Chapter 2 Lecture Notes

Up until this point, we have basically been using the fact that energy is conserved to balance work, heat and the various parameters that are changed when work is done or when heat enters or leaves the system. This is half the problem. The first law of thermodynamics tells us what is energetically allowable. However, the first law gives us no clue what processes will actually occur and which ones will not. For that matter, why does anything ever happen at all? The universe is an isolated system after all. There is no change in internal energy. There is no heat transferred in or out and no work is done on or by the system as a whole. q=0; w=0; DU=0. Sounds like a pretty boring place. Yet it isn't. Stars come into existence blow up, planets hurl around them and life evolves. Why? What is driving all of this? You can't say that it leads to a lower energy for the universe as a whole. That does not change.

Ok, let's look at some simple processes and try and understand what makes things change from one state to another. First consider an elastic ball (a perfect one in a vacuum, if you don't mind). If I drop the ball and it bounces, it will come back up to my hand. What has happened? The potential energy due to gravity is converted into kinetic energy on the way down and back to potential energy on the way back up again.

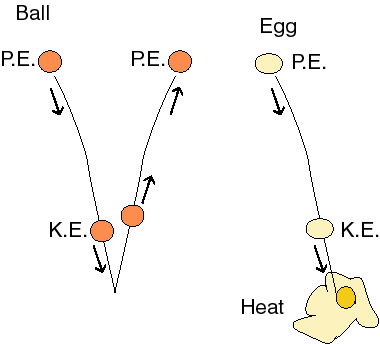
Everything is just as the first law said it should be. We convert energy from one form to another, conserving it. The initial state and the final state are energetically the same. But what if we used an egg? It goes down, but does not come back up. The initial and final states are not the same. We appear to have lost energy in the process. But this is not possible, according to the first law. So where did the energy go? It went into the random motion of molecules. It went into heat. We lost the ability to do work (the mass of the egg in the earth's gravitational field could have been used to move something against a force) and we ended up with random disorganized motion and a less organized state of matter. Apparently, the universe tends towards more random, disorganized states. This is a rather loose statement of the second law of thermodynamics and our way of quantitating the disorder and randomized motion in one state versus another is a state function called entropy. Increasing entropy means increasing disorder and randomized motion.

Every star that burns, every planet whose orbit is slowly decaying, every breath you take and calorie you metabolize brings the universe closer and closer to the point when the entropy is maximized, organized movement of any kind ceases, and nothing ever happens again. There is no escape. No matter how magnificent life in the universe becomes or how advanced, the slow increase in entropy cannot be stopped and the universe will eventually die.

Without the second law, nothing would ever happen at all. With it, the universe is doomed. Darn.

On that note, lets work our way through chapter 4.

Thermal motion is random. The probability that a bunch of randomly moving molecules will all suddenly start moving in the same direction is very small. Thus you generally cannot take full advantage of the kinetic energy in these molecules. The more of your energy that is contained as random kinetic energy (heat) the less efficiently it can be used to do work.

One obvious question is, if the universe is steadily moving towards a state of greater and greater disorder, how do highly ordered things, such as crystals or people, come about? Think about yourself. In order to provide the energy to maintain the order required of a living creature, you must consume food. The vast majority of the energy that you take in is converted to heat, greatly increasing the entropy of the universe. In fact, you can say that life evolved because living things are so efficient (pound for pound) at increasing entropy. Humans are incredibly good at increasing entropy, because they have devised so many ways of taking resources (ordered things like minerals, oil, food) and processing them, often to form other ordered things, but at the cost of creating much disorder in the process. You could view natural selection as selection for things that are most efficient at increasing entropy. This, then, is the meaning of life… to increase the entropy of the universe.

On cleaning one's room.

 The word "spontaneous" has a special meaning in physical chemistry. It has little to do with an impromptu gesture, a witty saying or impulsive shopping. It means a process that results in a change from one state to another in an irreversible way. Anything that happens in the universe that results in an irreversible change in state is spontaneous. As you can see, spontaneous is closely related to the words reversible and irreversible. A reversible change is not spontaneous. In fact, truly reversible processes do not happen in reality, because in a truly reversible process all forces would be perfectly balanced and there would be no driving force for the system to move. Of course by moving things very slowly always keeping forces in near perfect balance, we can approximate reversible processes to whatever degree we like, and this is what is usually referred to when we talk of a reversible process or a reversible path. For example, during reversible expansion of a gas, we keep the pressures essentially the same on the inside and the outside. Of course, if this was strictly true, the gas would not have any driving force to expand and nothing would ever happen. However, we can make it as close to true as we like by making the imbalance as small as we want. The process may take a very long time to occur, but, hey, this is theory and we have all the time in the universe. All things that actually happen in reality are irreversible processes. This just means that you could not reverse the process without converting at least some energy into random motion (and thus essentially make that energy less useful) in the process. Irreversible processes are always spontaneous. We will talk a lot about reversible and irreversible paths. The meaning is that for a reversible path, we stay almost perfectly in balance between opposing forces and for an irreversible path, we allow forces to be substantially out of balance.

For any spontaneous or irreversible process, there is a net increase in disorder, a net increase in entropy. This is the second law of thermodynamics. We now must put this in more quantitative terms. Quantitatively, we define entropy as follows:

Ok, where did that one come from? Why would a change (in this case infinitesimal change) in heat divided by temperature be a measure of the change in disorder?

What this expression means is that if we perform some process along a reversible path,  then the entropy produced should be proportional to the amount of heat produced (or consumed) and inversely proportional to the temperature. In order to understand this, let's look at an example:

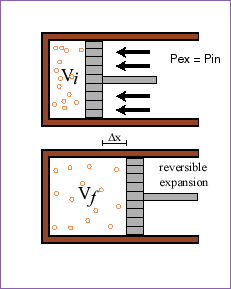
 Here is an isothermal, reversible expansion. The force per area on the outside (the outside pressure) is always kept as close as possible to the inside pressure as the piston slowly expands. Because the process results in work being performed by the system, for an ideal gas (click on the equation for an explanation), and because for an isothermal ideal gas DU = 0, we know that q = -w and so the amount of heat which comes in is just . Now let's think about this. In this context, I would like to rewrite the definition of entropy in a form that I think is much easier to think about:

Let’s go ahead and integrate this just to make it easier to think about – for finite changes:

What this says is that for our isothermal reversible expansion, the heat depends on two parts. First it depends on the temperature. This makes sense because temperature is a measure of the overall kinetic energy of the system. The higher the overall kinetic energy is, the more energy we are going to have to transfer in to maintain that high temperature (obviously if the temperature started at absolute zero and we did the expansion, we would not need to put heat into the system in order to keep it from getting any colder). But let’s now compare this equation to the one above for the reversible isothermal expansion (slightly rearranged):

We can now see why entropy is defined in such a funny way. In this case, the entropy is just the part of the equation that that deals with the fact that there is more room for the molecules in the final state than in the initial state. Assuming that the temperature is not zero, the molecules will occupy that added space (nature abhors a vacuum) by simple probability. This is what entropy embodies: it is the tendency of particles with kinetic energy (that are moving) to randomly occupy all the space available to them. More generally, it is the tendency of a system to explore all available states (this is the thermodynamic definition of disorder). What is actually accomplished (work performed or heat transferred) depends on both the entropy change and the temperature. By the way, the expression that we get for the isothermal expansion above,

actually works for any isothermal expansion of an ideal gas (whether the path is reversible or not). Why? Entropy is a state function. Therefore it does not matter how we get from one state to another. We can choose to use a reversible path as we did above and still must get the same result as we would for any other path.

I realize this is not a complete answer to why we choose the definition for entropy changes that we did, but it starts to make some sense that if we define entropy in this way it ends up being the part of the equation that deals with the total number of states available to the system. It turns out that this will always be true. Entropy defined in this way will end up being proportional to the log of the fractional change in the number of states available in the system. The reason why we use a log instead of the change in the fractional change in the number of states itself is that the log ends up being proportional to energy. We will come back to this a bit later.

We mentioned the issue of probability and the relationship between entropy and the probability of particles occupying the available space. Let's look at a tutorial for more information.

Understanding the second law and the relationship between entropy and enthalpy:

Let’s now think about what is happening in the surroundings. You can think of the surroundings in the same way as the system except that it is so large that we consider it to be isothermal and generally speaking, we consider it to be at constant pressure. Ok, now the following argument is critical so pay attention. Because the surroundings are at constant pressure, q_sur = DH_sur. That means that the heat transferred to the surroundings is equal to a state function and is independent of the path that the heat used to get out into the surroundings (this is always true for the surroundings). Thus we can always choose to consider it as having been transferred by a reversible path. Looking at it another way, the surroundings are generally assumed not to change state when something happens in the system, thus transfer of heat to and from the surrounds is effectively reversible (since there is no change of state, we cannot say that the change was irreversible). Therefore we can say that for the entropy change of the surroundings,

regardless of how the heat got to the surroundings. So, this equation (dq = TdS or in integrated form, q = TDS) is always true for the surroundings, but only true for the system in the specific case of a reversible change in the system. (Note that q_sur = -q_sys. Most of the time when we say q, we mean q_sys. You need to keep the signs straight.) What are the consequences of this? Well for a reversible change in the system, the heat coming from the system has the opposite sign from the heat going to the surroundings (or the other way around) but the same magnitude. Thus for an isothermal reversible change:

In other words, for a reversible change in the system, the total entropy change (system and surroundings) is zero. However, if the change in the system is irreversible (spontaneous), this will not be true. To understand what will happen, lets again consider the piston system. This time, we will compare the isothermal reversible expansion to an isothermal expansion against a fixed pressure that is equal to the final pressure in the case of the reversible expansion.

If we allow the piston to expand against a pressure P_F from the very beginning (not reversibly) until the inside pressure is P_F:

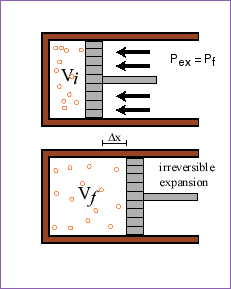
Recall that for a reversible expansion . Let's compare how much work is done in the two cases. For example, let's take V_F =2V_I. In the first case (irreversible) this gives . The reversible case gives w_rev = -(0.693)nRT. So, more work is done on the surroundings in the reversible case than in the irreversible case. Since both cases are isothermal ideal gases, we know that q = -w (since the internal energy change is zero). This means that more heat is taken up by the reversible expansion than the irreversible one. Ok, now here is the trick. The entropy of the system associated with the expansion is a state function and is independent of path. Thus, it is the same whether the expansion is done reversibly or irreversibly and is always DS_sys = q_rev/T = (0.693nRT)/T = 0.693nR. But the entropy change in the surroundings depends only on the amount of heat transferred. This is therefore different for the reversible and the irreversible cases. DS_sur,rev = (0.693nRT/T) = 0.693nR, but DS_sur,irrev = (0.5nRT)/T = 0.5nR. In the reversible case, the total entropy change for the system and the surroundings is zero (the two terms cancel because the heat terms have different signs). In the irreversible case, they do not cancel and the total entropy change ends up being positive, DS = 0.193nR. This result is general. The total entropy change for any irreversible reaction (a spontaneous reaction) is greater than zero. This is just another way of stating the second law of thermodynamics. It follows directly from this argument that the change in entropy for the system is greater than or equal to q/T.

For the spontaneous (forward irreversible) reaction,

For a reversible reaction,

In general,

This is called the Clausius Inequality (here q is the usual q defined in terms of the system, not in terms of the surroundings). To get a molecular view of where these ideas come from, consider this tutorial on gases and the probability of gases occupying available space.

Now finally, lets add the entropy change for the system with the entropy change for the surroundings and see what we get in general:

DS_tot = DS_sys + DS_sur

Remember above that we said that for the surroundings it was always true that q_sur = TDS_sur because heat transfer to the surroundings does not change the state of the surroundings and therefore we can choose a reversible path. Now, remember the heat transferred to or from the surroundings has the opposite sign (but same magnitude) of the heat transferred to or from the system. Therefore, q = -q_sur and we can write q = -TDS_sur (q without the subscript is q for the system). Rearranging, this means that the entropy change for the surroundings is always just DS_sur = –q/T. Now lets plug this into the equation for total entropy change:

DS_tot = DS_sys + –q/T

But we know from above that:

Comparing these two equations we see that:

DS_tot is greater than or equal to zero

This is the second law of thermodynamics

If you are human, and have never seen this stuff before, you should be confused right now. Start over and work through it again. This is the central and most useful concept in thermodynamics. Below, we are going to multiply DS_tot by –T and give it a new name, the Gibbs free energy. We will take DS_sur and multiply it by T and (at constant pressure) get the enthalpy of the system. Then suddenly we will have the relationship between DG, DH and DS that you learned in freshman chemistry (DG = DH - TDS). All the rest of equilibrium thermodynamics at constant pressure falls out of this equation. But I am getting ahead of myself…

A Subtle Confusion

The above example is a good one, but can lead to some confusion. In the end, we seem to be saying that the total entropy change for a process is not a state function. In other words, it appears that the total entropy change depends on whether we choose a reversible or irreversible path for expansion of the piston. It actually doesn’t if you really include everything in the calculation. In fact there is no way to go from the compressed to the expanded state without either doing something irreversible (generating excess heat) or decreasing the entropy of some other system in the process. What has been left out of the argument above is, what was the nature of the work done in the reversible case? What was it pushing on that perfectly matched the pressure inside during the expansion? It could have been my arm, but that would have resulted in excess generation of heat and we would be back to the irreversible case. If you used the energy to compress some other gas, you would simply be decreasing the entropy of that system in just the opposite way that you increased the entropy of the expanding system. So the total entropy in fact is the same regardless of how you do the expansion if you actually take into account what the work is being done on. The bottom line is that expansion of a compressed gas is in fact a spontaneous reaction and therefore the total entropy change will be positive and independent of path. We have artificially made it reversible by storing the energy somewhere else in an equal and opposite reaction; we did not lose the capacity to do work in the process. But this in fact requires an entropy decrease in some other system that we have not taken into account. The problem in trying to come up with a good example is that nothing that changes the state of the universe is reversible. So you can’t really talk about a real process that takes place by itself and is reversible.

Back to lecture…

The argument for the definition of entropy and its relationship to the second law given above is a tricky one to understand completely. The total entropy change for a process tells you whether it is spontaneous or not. A positive total entropy change means the process will happen. A negative total entropy change means the process will not happen (in fact, the opposite will happen -- it will run the other way). A zero total entropy change for a process means that it is in equilibrium, and nothing will happen. Take whatever time you need to understand the last few paragraphs. On this rests almost the remainder of what we will do this semester. If you are still confused, try going through the ideas more slowly using the following interactive tutorial. This tutorial is based on questions and discussions I frequently have with students in my office on this subject.

Next let's explore the relationship between entropy and work a bit more in yet another tutorial.

Above I have stated that entropy is a state function, but I have given no proof of this. You can understand this in terms of something called a Carnot cycle, but I want to put off discussion of the Carnot cycle for now; just realize that at constant pressure and temperature, q_rev = DH and the enthalpy change we know is a state function. Since T is constant, this means that q_rev/T will be independent of path as well. So at least under these conditions, the entropy is a state function. This turns out to be more general, but the above argument shows this in at least one common condition and will do for now.

Now let's start considering various examples of spontaneous processes. The first is the transfer of heat from a hot body to a cold body. We all know that this is spontaneous, but now we have the formalism to quantitate this.

What is the entropy change on the hot side? Consider the transfer of a small amount of heat, dq. This amount of heat is not large enough to significantly change the temperature of either side. Thus, the transfer of the heat does not really change the state of the system and is like transferring heat in or out of the surroundings. Thus, dS=dq/T on both sides (you can think of it as being “locally reversible” even though the whole reaction is not reversible). Since the heat goes out of the left, that q is negative. It is positive on the right because heat is going in. The total entropy change is thus, dS_tot = dq/T_c - dq/T_h. Because T_c < T_h, the total entropy change for the process is positive. It is indeed spontaneous, as we already knew from our experience. If you wanted to perform this calculation for a large amount of heat, say the amount required to reach thermal equilibration, you would have to do an integral for each side of dS = dq/T over the temperature ranges involved. More on this later.

Here is another example. I find it easier to think about entropy in terms of some concrete process than in abstract terms.

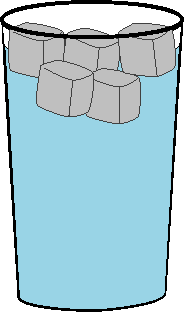Let's consider a phase transition. When you raise the temperature above 0 C, ice melts and therefore this must have a positive entropy change associated with it. Consider the glass of ice water to the left. Here, an equilibrium has been established between ice and liquid. In order to pull the attractive ice molecules apart, energy must come from the kinetic energy of either the water molecules themselves or the surroundings. This is the enthalpy of fusion. Since our glass is open to the atmosphere, it is at constant pressure. Therefore the heat is just equal to the enthalpy of fusion or q_P = DH. Since the ice and the water are at equilibrium (the forces pushing the ice towards melting are equal to those pushing the water towards freezing), we can say that any small amount of ice that goes to liquid or liquid that goes to ice, does so reversibly. Thus, the change in entropy for this process is given by:. Of course you realize that it does not really matter how the ice melts (what path it takes) since entropy is a state function. What does matter for this particular expression is that the system be isothermal (ice water is very isothermal). If it was not isothermal, one would have to do the problem in steps -- an isothermal change in phase, followed by warming or heating of the water or ice that results. In fact let's do this. Instead of ice water, lets consider the entropy changes for putting an ice cube in a glass of warm water and letting it melt (assume it is a well insulated glass -- adiabatic). The water starts at T_initial. What is the easiest way to do this? First calculate what the entropy change is to cool the water to 0C by reversibly removing heat from the system (we will assume that the ice is initially at 0 C in this case). Next, calculate the amount of heat at that temperature you would have to add to the system to melt the ice cube. Next calculate the difference between the two amounts of heat and add back the remaining heat so that the total heat lost or gained is zero (adiabatic) and determine the amount of entropy change which occurs during that process:

At each step, the infinitesimal entropy change for the system is just dq divided by the temperature. For the cooling and heating of the water, we must integrate over the temperature range, since the temperature is not constant. In step one, we have an entropy decrease for the system as the water is cooled:

.

For step two, we melt the ice at the temperature of 0 C (T_fus), so

.

Finally, for the third step, we balance the heat by (in this example) adding an amount of heat -(q₁ + q_fus) back into the glass (note that since the ice cube melted completely, that means that it one would have to remove more heat to cool the glass to 0 C than you would have to add in order to melt the ice -- if this was not true, the ice cube would not melt completely). This will cause an increase in entropy:

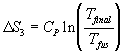
But how do we find T_final? We know that the system is adiabatic. Thus the total heat must be zero. This means that q₃ = -(q₁ + q₂). Thus the final temperature will just be T_final = T_fus + q₃/C_P. One final question, is this process spontaneous? Of course we know that it is (stick an ice cube in your hot tea and it melts). Can we show this? To do so, all we have to do is to show that the total entropy change (the system plus the surroundings) is positive. The entropy change of the system we know is DS₁ + DS₂ + DS₃ . Try this example for an initial temperature of 60 C, 5 grams of ice and 100 mls of water (remember the change in the amount of water due to the ice melting). Given the C_P of water is 75.6 J/(mole K) and the enthalpy of fusion is 6.01 kJ/mole, I get a final temperature of about 53.4 degrees and an overall entropy change of 1.39 J/K for the system (the entropy change for cooling the water was -83.51 J/K, for melting the ice was 6.113 J/K and for warming the water back up afterwards was 78.79). How about the surroundings? Zip. The system is adiabatic so no heat is transferred to the surroundings so dq/T is zero. This is an important example. Go over it until you understand it. Now try the problem again, except assume that it is isothermal instead of adiabatic. Same deal, except that at the last step you must add enough heat to bring it back to the original temperature. Without doing the calculation, you should be able to tell me whether the overall entropy (system and surroundings) will be more or less positive. Does this match your experience? (think about putting the glass in a very large bath of water at 60 C -- do you think there is more or less driving force for the ice in the glass to melt vs. the glass being completely insulated). If you would like to do well on the next test, make sure you understand this way of doing things and be able to apply it to any of a number of situations!

Now let's run through a few examples of changes in state and the associated entropy changes for the system:

Vary the temperature but the volume is constant:

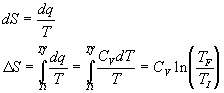
Vary the temperature at constant pressure:

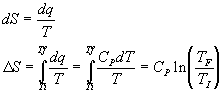
The above two equations are general and depend only on C_V or C_P being temperature independent over the temperature range in question.

The next ones are only good for ideal gases. For an isothermal expansion (change the volume at constant temperature):

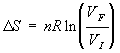
This was derived previously from the reversible work for an ideal gas. We can also put this in terms of initial and final pressures just by using the gas law and realizing that V_F and V_I are inversely related to P_F and P_I for constant temperature and a closed system:

What do you do when you are given an ideal gas problem and both T and P or T and V change? Simple, do it in two steps. First change the T holding either the V or the P constant, then change V or P (depending on what you are given). Remember that if you know two of these values (T, V and P) in a closed system that you know the third (this is true for any system, ideal or not). Thus, if you change T and V to the final values and calculate the entropy for those two steps, you know that P must already be at its final value to satisfy the equation of state for the system and therefore you do not have to worry about changing it. Conversely, if it is more convenient, you could change T and then P and you would know that V would be in its final state after you were through and you would not have to worry about V.

I am not very worried about absolute entropy. It is not particularly useful. I am also not too worried about thermodynamic temperature. It is historically interesting but not very conceptually illuminating.

We can do the same kind of thermodynamic bookkeeping for entropy that we did for enthalpy. We can add, subtract, and reverse entropy changes just like enthalpy changes. Also, like enthalpies, we can talk about a reference entropy of a compound and use this to calculate entropy changes for reactions. For enthalpies, this was the enthalpy of formation. We added them up using the right stochiometries and signs to get the enthalpy change for the whole reaction, right? Same deal for entropy changes except we call it the molar entropy. I am not going to worry about this because no one really uses this to calculate thermodynamics for reactions. Later on, we will talk about something called a chemical potential which embodies the same idea and is much more useful.

The Gibbs Free Energy

Ok, now this next bit is very important. Remember that we have said that if the overall entropy change for the system is positive, then the process in question is spontaneous and if it is zero the process is in equilibrium and if it is negative then the process is spontaneous in the reverse direction. We are now going to look hard at this and define a new state function based on the total entropy change that will tell us not only whether a reaction will go forwards, backwards or nowhere, but also how far the reaction or process will go one way or the other. So, we said above that the overall entropy, dS_tot is just dS_sys + dS_surroundings. But remember that the entropy change in the surroundings is always just the heat that enters the surroundings divided by the temperature. Now, what is this heat? At constant volume it is dq_V = dU. At constant pressure it is dq_P = dH. Therefore we can say that at constant volume, dS_surroundings = -dU_sys/T and at constant pressure dS_surroundings = -dH_sys/T. Note that these are the internal energy changes and enthalpy changes for the system, not for the surroundings. Thus, a positive enthalpy, for example, means that heat is leaving the surroundings, giving the minus sign. Therefore:

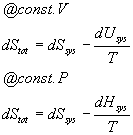
Multiplying both sides by -T gives:

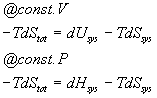
T is always positive. Therefore, if the reaction is going to go forwards, the -TdS_tot term will always be negative and for a reaction in equilibrium it will be zero and for a reaction which is spontaneous in the opposite direction it will be positive. Furthermore, this term has units of energy and is related directly to the amount of energy available to do work if the work was coupled to the process in question. At constant volume we call this the Helmholz free energy and symbolize it with an A. At constant pressure, we call this the Gibbs free energy and symbolize it with a G. We have :

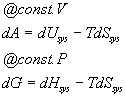
These equations are more familiar in their integrated forms (assuming that T is constant):

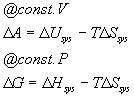
These suggest general definitions for G and A: A = U - TS and G = H - TS. We will use the Gibbs free energy a great deal in the coming weeks. The Helmholz free energy we will not use except for completeness (your book does not even mention it so I will not hold you responsible for it).

For another example of the way entropy and enthalpy work together to determine the Gibbs free energy and whether a process is spontaneous or not see the following tutorial.

The Carnot Engine, a classic example

The classic example of how to do problems involving entropy changes and work is called the Carnot Cycle. It is a heat engine, similar in many ways to your refrigerator or your air conditioner. Run in the way shown, it is the most efficient possible means of running a heat engine. So, let's try and understand how this cycle works and what it tells us about the efficiency of many different types of heat pumps and engines. Here are two tutorials about the Carnot cycle. One is general and goes through a scheme like this. Note that this tutorial was written with reference to another book and you are not responsible for the calculation of work and efficiency of the total cycle… I just left that in case you were interested. Just look at the calculations of the thermodynamic parameters at each step. This is good practice for using what you have learned. The other is an example of a heat engine run in this way.