Table for CAN(3,k,11) for k up to 10000

Last Updated Thu Jan 5 06:12:57 MST 2012

Locate the k in the first column that is at least as large as the number of factors in which you are interested. Then let N be the number of rows (tests) given in the second column. A CA(N;3,k,11) exists according to a construction in the reference (cryptically) given in the third column. The accompanying graph plots N vertically against log k (base 10).

Change t: - + Change v: - + or go to Global Menu.

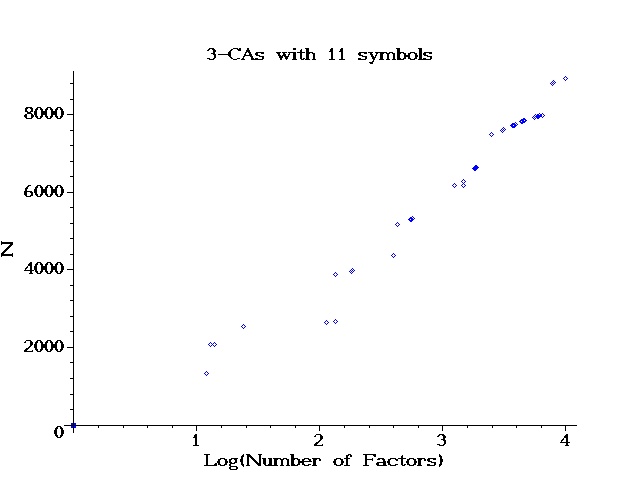
k N Source 12 1331 orthogonal array 13 2079 orthogonal array fuse fuse postop NCK 14 2088 orthogonal array fuse fuse postop NCK 24 2541 Chateauneuf-Kreher doubling 50 2651 Sherwood-Martirosyan-Colbourn 132 3751 Colbourn-Martirosyan-Trung-Walker 146 3971 Sherwood-Martirosyan-Colbourn 398 4378 Cyclotomy (Colbourn) 419 4609 Cyclotomy (Colbourn) 420 5819 Add a factor 550 6171 Colbourn-Martirosyan-Trung-Walker 600 6402 Cohen-Colbourn-Ling 602 7222 Cyclotomy (Colbourn) fuse 1452 7271 Colbourn-Martirosyan-Trung-Walker 1573 7491 Colbourn-Martirosyan-Trung-Walker 1584 7581 Colbourn-Martirosyan-Trung-Walker 1606 7701 Colbourn-Martirosyan-Trung-Walker 1694 8108 Colbourn-Martirosyan-Trung-Walker 1705 8198 Colbourn-Martirosyan-Trung-Walker 1752 8206 Cohen-Colbourn-Ling 1848 8208 Colbourn-Martirosyan-Trung-Walker 1881 8268 Colbourn-Martirosyan-Trung-Walker 1947 8278 Colbourn-Martirosyan-Trung-Walker 1980 8288 Colbourn-Martirosyan-Trung-Walker 2101 8298 Colbourn-Martirosyan-Trung-Walker 2112 8308 Colbourn-Martirosyan-Trung-Walker 2233 8398 Colbourn-Martirosyan-Trung-Walker 2321 8458 Colbourn-Martirosyan-Trung-Walker 2442 8468 Colbourn-Martirosyan-Trung-Walker 2464 8478 Colbourn-Martirosyan-Trung-Walker 2475 8518 Colbourn-Martirosyan-Trung-Walker 2508 8528 Colbourn-Martirosyan-Trung-Walker 2552 8548 Colbourn-Martirosyan-Trung-Walker 2596 8558 Colbourn-Martirosyan-Trung-Walker 2805 8608 Colbourn-Martirosyan-Trung-Walker 2838 8618 Colbourn-Martirosyan-Trung-Walker 2849 8658 Colbourn-Martirosyan-Trung-Walker 2860 8668 Colbourn-Martirosyan-Trung-Walker 2882 8678 Colbourn-Martirosyan-Trung-Walker 2904 8688 Colbourn-Martirosyan-Trung-Walker 2970 8698 Colbourn-Martirosyan-Trung-Walker 3212 8728 Colbourn-Martirosyan-Trung-Walker 3223 8778 Colbourn-Martirosyan-Trung-Walker 3256 8788 Colbourn-Martirosyan-Trung-Walker 3344 8798 Colbourn-Martirosyan-Trung-Walker 3355 8848 Colbourn-Martirosyan-Trung-Walker 3399 8858 Colbourn-Martirosyan-Trung-Walker 3476 8868 Colbourn-Martirosyan-Trung-Walker 3564 8898 Colbourn-Martirosyan-Trung-Walker 3696 8908 Colbourn-Martirosyan-Trung-Walker 3828 8928 Colbourn-Martirosyan-Trung-Walker 3960 8938 Colbourn-Martirosyan-Trung-Walker 4125 8948 Colbourn-Martirosyan-Trung-Walker 4257 8958 Colbourn-Martirosyan-Trung-Walker 4356 8968 Colbourn-Martirosyan-Trung-Walker 4378 8978 Colbourn-Martirosyan-Trung-Walker 4532 9209 Colbourn-Martirosyan-Trung-Walker 4576 9219 Colbourn-Martirosyan-Trung-Walker 4609 9229 Colbourn-Martirosyan-Trung-Walker 4776 9339 Cohen-Colbourn-Ling 5028 9570 Cohen-Colbourn-Ling 5040 10780 Cohen-Colbourn-Ling 6050 10791 Colbourn-Martirosyan-Trung-Walker 6600 11022 Colbourn-Martirosyan-Trung-Walker 7150 11242 Cohen-Colbourn-Ling 7200 11363 Cohen-Colbourn-Ling 7300 11662 Cohen-Colbourn-Ling 10000 11891 Colbourn-Martirosyan-Trung-Walker

Graph: