Table for CAN(3,k,17) for k up to 10000

Locate the k in the first column that is at least as large as the number of factors in which you are interested. Then let N be the number of rows (tests) given in the second column. A CA(N;3,k,17) exists according to a construction in the reference (cryptically) given in the third column. The accompanying graph plots N vertically against log k (base 10).

Go to Global Menu.

Change t: - +

Change v: - +
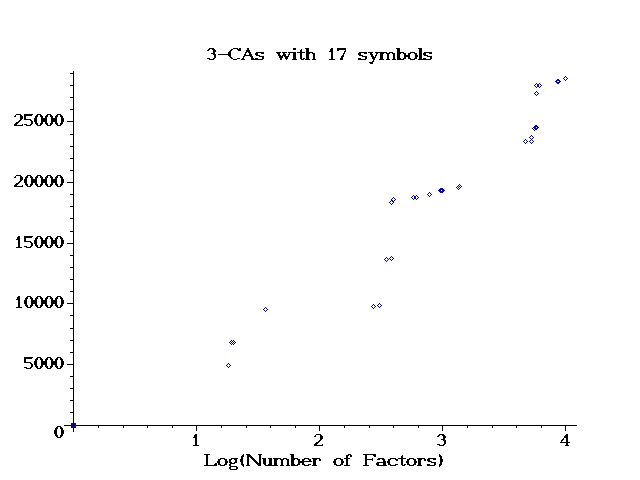
kNSource
184913orthogonal array
206855fuse symbols
369537Chateauneuf-Kreher doubling
4012551Chateauneuf-Kreher doubling
30614161Colbourn-Martirosyan-Trung-Walker
34017175Colbourn-Martirosyan-Trung-Walker
34217909Colbourn-Martirosyan-Trung-Walker
38019851fuse symbols
52722113Colbourn-Martirosyan-Trung-Walker
54422369Colbourn-Martirosyan-Trung-Walker
56122625Colbourn-Martirosyan-Trung-Walker
57822881Colbourn-Martirosyan-Trung-Walker
61223137Colbourn-Martirosyan-Trung-Walker
64823698Cohen-Colbourn-Ling
68026151Colbourn-Martirosyan-Trung-Walker
72026712Cohen-Colbourn-Ling
520227761Colbourn-Martirosyan-Trung-Walker
549130775Colbourn-Martirosyan-Trung-Walker
550831031Colbourn-Martirosyan-Trung-Walker
578031847Colbourn-Martirosyan-Trung-Walker
581432581Colbourn-Martirosyan-Trung-Walker
610334523Colbourn-Martirosyan-Trung-Walker
642634555Colbourn-Martirosyan-Trung-Walker
646034571Colbourn-Martirosyan-Trung-Walker
673236833Colbourn-Martirosyan-Trung-Walker
678337857Colbourn-Martirosyan-Trung-Walker
714037889Colbourn-Martirosyan-Trung-Walker
748037905Colbourn-Martirosyan-Trung-Walker
749737921Colbourn-Martirosyan-Trung-Walker
785437937Colbourn-Martirosyan-Trung-Walker
822837953Colbourn-Martirosyan-Trung-Walker
895939041Colbourn-Martirosyan-Trung-Walker
924839297Colbourn-Martirosyan-Trung-Walker
946939553Colbourn-Martirosyan-Trung-Walker
953739809Colbourn-Martirosyan-Trung-Walker
977540065Colbourn-Martirosyan-Trung-Walker
982640321Colbourn-Martirosyan-Trung-Walker
1000040577Colbourn-Martirosyan-Trung-Walker
 Graph: