Table for CAN(3,k,2) for k up to 10000

Last Updated Thu Jan 5 06:12:57 MST 2012

Locate the k in the first column that is at least as large as the number of factors in which you are interested. Then let N be the number of rows (tests) given in the second column. A CA(N;3,k,2) exists according to a construction in the reference (cryptically) given in the third column. The accompanying graph plots N vertically against log k (base 10).

Change t: - + Change v: + or go to Global Menu.

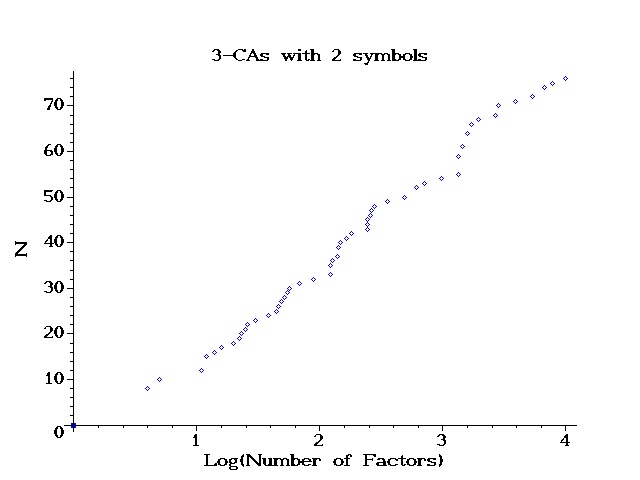
k N Source 4 8 orthogonal array 5 10 Derive from strength 4 11 12 Derive from strength 4 12 15 tabu search (Nurmela) 14 16 Sloane 16 17 Derive from strength 4 20 18 Chateauneuf-Kreher doubling 22 19 Chateauneuf-Kreher doubling 23 20 simulated annealing (Torres+Rodriguez) 25 21 simulated annealing (Torres+Rodriguez) 26 22 simulated annealing (Torres+Rodriguez) 28 23 simulated annealing (Torres+Rodriguez) 38 24 simulated annealing (Torres+Rodriguez) 44 25 simulated annealing (Torres+Rodriguez) 46 26 simulated annealing (Torres+Rodriguez) 49 27 simulated annealing (Torres+Rodriguez) 52 28 simulated annealing (Torres+Rodriguez) 54 29 simulated annealing (Torres+Rodriguez) 56 30 simulated annealing (Torres+Rodriguez) 68 31 simulated annealing (Torres+Rodriguez) 88 32 Power CT11^2,T3c 121 33 Power CT11^2 123 35 simulated annealing (Torres+Rodriguez) 127 36 simulated annealing (Torres+Rodriguez) 140 37 simulated annealing (Torres+Rodriguez) 141 39 simulated annealing (Torres+Rodriguez) 144 40 simulated annealing (Torres+Rodriguez) 156 41 simulated annealing (Torres+Rodriguez) 177 42 simulated annealing (Torres+Rodriguez) 242 43 simulated annealing (Torres+Rodriguez) 243 44 simulated annealing (Torres+Rodriguez) 246 45 simulated annealing (Torres+Rodriguez) 256 46 simulated annealing (Torres+Rodriguez) 257 47 simulated annealing (Torres+Rodriguez) 280 48 simulated annealing (Torres+Rodriguez) 352 49 Power CT11^3T7T3c 484 50 Power CT11^3,T7c 605 52 Power CT11^3,T6c 704 53 Power CT11^3T3T3c 968 54 Power CT11^3,T3c 1331 55 Power CT11^3 1332 59 Add a factor 1452 61 Power CT12^3,cT1T1 1584 64 Power CT12^3,cT1 1712 66 simulated annealing (Torres+Rodriguez) 1936 67 Power CT11^4T7T7c 2662 68 Power CT11^4,cT9c 2816 70 Power CT11^4T3cT3cT7c 3872 71 Power CT11^4T7T3c 5324 72 Power CT11^4,T7c 6655 74 Power CT11^4,T6c 7744 75 Power CT11^4T3T3c 10000 76 Power CT11^4,T3c

Graph: