Table for CAN(3,k,6) for k up to 10000

Last Updated Thu Jan 5 06:12:57 MST 2012

Locate the k in the first column that is at least as large as the number of factors in which you are interested. Then let N be the number of rows (tests) given in the second column. A CA(N;3,k,6) exists according to a construction in the reference (cryptically) given in the third column. The accompanying graph plots N vertically against log k (base 10).

Change t: - + Change v: - + or go to Global Menu.

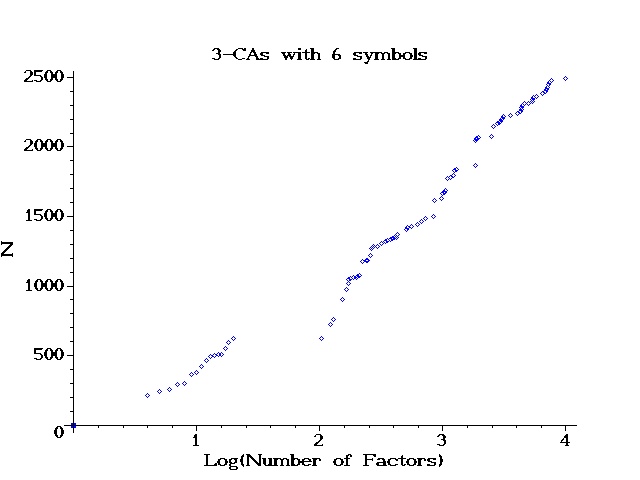
k N Source 4 216 Derive from strength 4 5 240 cross-sum (CKRS) 6 258 cross-sum (CKRS) 7 293 simulated annealing (CKRS) 8 304 simulated annealing (CKRS) 9 379 simulated annealing (CKRS) 10 393 simulated annealing (CKRS) 12 463 Chateauneuf-Kreher doubling 13 494 Chateauneuf-Kreher doubling postop NCK 14 498 Chateauneuf-Kreher doubling postop NCK 15 508 Chateauneuf-Kreher doubling postop NCK 16 510 Chateauneuf-Kreher doubling postop NCK 17 604 Chateauneuf-Kreher doubling postop NCK 18 608 Chateauneuf-Kreher doubling postop NCK 104 624 Cyclotomy (Colbourn) 109 654 Cyclotomy (Colbourn) 128 762 Cyclotomy (Colbourn) 139 834 Cyclotomy (Colbourn) 152 906 Cyclotomy (Colbourn) 157 942 Cyclotomy (Colbourn) 158 972 Cyclotomy (Colbourn) 164 978 Cyclotomy (Colbourn) 168 1044 Chateauneuf-Kreher doubling 172 1049 Chateauneuf-Kreher doubling 178 1054 Chateauneuf-Kreher doubling 186 1059 Chateauneuf-Kreher doubling 194 1064 Chateauneuf-Kreher doubling 198 1069 Chateauneuf-Kreher doubling 208 1074 Chateauneuf-Kreher doubling 214 1114 Chateauneuf-Kreher doubling 218 1119 Chateauneuf-Kreher doubling 226 1227 Chateauneuf-Kreher doubling 240 1232 Chateauneuf-Kreher doubling 248 1237 Chateauneuf-Kreher doubling 256 1242 Chateauneuf-Kreher doubling 260 1302 Cohen-Colbourn-Ling 276 1308 Cohen-Colbourn-Ling 300 1314 Cohen-Colbourn-Ling 312 1320 Cohen-Colbourn-Ling 316 1326 Cohen-Colbourn-Ling 320 1332 Cohen-Colbourn-Ling 328 1338 Cohen-Colbourn-Ling 336 1344 Cohen-Colbourn-Ling 344 1350 Cohen-Colbourn-Ling 356 1356 Cohen-Colbourn-Ling 372 1362 Cohen-Colbourn-Ling 388 1368 Cohen-Colbourn-Ling 396 1374 Cohen-Colbourn-Ling 416 1380 Cohen-Colbourn-Ling 428 1422 Cohen-Colbourn-Ling 436 1428 Cohen-Colbourn-Ling 450 1435 Cohen-Colbourn-Ling 468 1442 Cohen-Colbourn-Ling 474 1449 Cohen-Colbourn-Ling 480 1456 Cohen-Colbourn-Ling 504 1460 Cohen-Colbourn-Ling 520 1467 Cohen-Colbourn-Ling 525 1470 Cohen-Colbourn-Ling 552 1474 Cohen-Colbourn-Ling 600 1481 Cohen-Colbourn-Ling 624 1488 Cohen-Colbourn-Ling 632 1495 Cohen-Colbourn-Ling 640 1502 Cohen-Colbourn-Ling 656 1509 Cohen-Colbourn-Ling 672 1516 Cohen-Colbourn-Ling 688 1523 Cohen-Colbourn-Ling 712 1530 Cohen-Colbourn-Ling 744 1537 Cohen-Colbourn-Ling 776 1544 Cohen-Colbourn-Ling 792 1551 Cohen-Colbourn-Ling 832 1558 Cohen-Colbourn-Ling 856 1602 Cohen-Colbourn-Ling 872 1609 Cohen-Colbourn-Ling 890 1705 Cohen-Colbourn-Ling 930 1713 Cohen-Colbourn-Ling 970 1721 Cohen-Colbourn-Ling 990 1729 Cohen-Colbourn-Ling 992 1731 Cohen-Colbourn-Ling 1040 1737 Cohen-Colbourn-Ling 1070 1783 Cohen-Colbourn-Ling 1090 1791 Cohen-Colbourn-Ling 1112 1810 Cohen-Colbourn-Ling 1116 1870 Cohen-Colbourn-Ling 1164 1879 Cohen-Colbourn-Ling 1188 1888 Cohen-Colbourn-Ling 1208 1896 Cohen-Colbourn-Ling 1248 1897 Cohen-Colbourn-Ling 1261 1910 Cohen-Colbourn-Ling 1287 1919 Cohen-Colbourn-Ling 1352 1928 Cohen-Colbourn-Ling 1391 1976 Cohen-Colbourn-Ling 1417 1985 Cohen-Colbourn-Ling 1424 1994 Cohen-Colbourn-Ling 1488 2004 Cohen-Colbourn-Ling 1552 2014 Cohen-Colbourn-Ling 1584 2024 Cohen-Colbourn-Ling 1664 2034 Cohen-Colbourn-Ling 1680 2068 Cohen-Colbourn-Ling 1722 2078 Cohen-Colbourn-Ling 1764 2088 Cohen-Colbourn-Ling 1806 2098 Cohen-Colbourn-Ling 1869 2108 Cohen-Colbourn-Ling 1953 2118 Cohen-Colbourn-Ling 2037 2128 Cohen-Colbourn-Ling 2079 2138 Cohen-Colbourn-Ling 2184 2148 Cohen-Colbourn-Ling 2247 2198 Cohen-Colbourn-Ling 2289 2208 Cohen-Colbourn-Ling 2392 2238 Cohen-Colbourn-Ling 2560 2270 Cohen-Colbourn-Ling 2688 2284 Cohen-Colbourn-Ling 3328 2298 Cohen-Colbourn-Ling 4032 2312 Cohen-Colbourn-Ling 4160 2326 Cohen-Colbourn-Ling 4416 2340 Cohen-Colbourn-Ling 4800 2354 Cohen-Colbourn-Ling 4992 2368 Cohen-Colbourn-Ling 5056 2382 Cohen-Colbourn-Ling 5120 2396 Cohen-Colbourn-Ling 5200 2403 Cohen-Colbourn-Ling 5248 2410 Cohen-Colbourn-Ling 5520 2418 Cohen-Colbourn-Ling 6000 2433 Cohen-Colbourn-Ling 6240 2448 Cohen-Colbourn-Ling 6320 2463 Cohen-Colbourn-Ling 6552 2464 Cohen-Colbourn-Ling 6760 2480 Cohen-Colbourn-Ling 10000 2492 Power CT100^2

Graph: