| k | N | Source |
| 20 | 47045881 | orthogonal array |
| 21 | 91485342 | extended OA (Colbourn) |
| 22 | 136055124 | Add 1 factors |
| 24 | 148035881 | orthogonal array fuse fuse fuse fuse |
| 25 | 188183467 | perfect hash family4,25,19,c |
| 27 | 188183520 | perfect hash family4,27,20 |
| 38 | 225325009 | double OA (Colbourn-Zhou) |
| 40 | 227794249 | double OA (Colbourn-Zhou) |
| 41 | 359028199 | Add 1 factors |
| 42 | 423412777 | perfect hash family9,42,19,c |
| 45 | 423412920 | perfect hash family9,45,20 |
| 47 | 470458639 | perfect hash family10,47,19,c |
| 51 | 470458800 | perfect hash family10,51,20 |
| 53 | 517504501 | perfect hash family11,53,19,c |
| 60 | 517504680 | perfect hash family11,60,20 |
| 64 | 564550560 | perfect hash family12,64,20 |
| 65 | 658642320 | perfect hash family14,65,20 |
| 95 | 705687949 | perfect hash family15,95,19,c |
| 96 | 705688200 | perfect hash family15,96,20 |
| 361 | 752733811 | perfect hash family16,361,19,c |
| 362 | 752734080 | Power CT19^2+1 |
| 363 | 968422194 | Add 1 factors |
| 364 | 1057555260 | Add 2 factors |
| 365 | 1144349046 | Add 3 factors |
| 366 | 1188918828 | Add 4 factors |
| 380 | 1233488341 | Add 19 factors |
| 381 | 1233488610 | Add 19 factors |
| 382 | 1473622200 | Add 19 factors |
| 515 | 1505467603 | perfect hash family32,515,19,c |
| 516 | 1505468160 | perfect hash family32,516,20 |
| 517 | 1850044446 | Add 1 factors |
| 518 | 2008108296 | Add 2 factors |
| 519 | 2070018720 | perfect hash family44,519,20 |
| 520 | 2117063809 | perfect hash family45,520,19,c |
| 522 | 2117064600 | perfect hash family45,522,20 |
| 523 | 2199350377 | Add 19 factors |
| 525 | 2199597301 | Add 19 factors |
| 529 | 2199720763 | Add 19 factors |
| 532 | 2199844225 | Add 19 factors |
| 534 | 2199967687 | Add 19 factors |
| 535 | 2199968244 | Add 19 factors |
| 722 | 2273305342 | Martirosyan-TVT |
| 723 | 2323554645 | Martirosyan-TVT variant |
| 724 | 2373803679 | Martirosyan-TVT |
| 726 | 2673933645 | Martirosyan-TVT |
| 728 | 2845292403 | Martirosyan-TVT |
| 730 | 2974310193 | Martirosyan-TVT |
| 734 | 2996903470 | Add 19 factors |
| 739 | 2997026932 | Add 19 factors |
| 741 | 2997150394 | Add 19 factors |
| 742 | 3047399697 | Add 19 factors |
| 760 | 3105673492 | Martirosyan-TVT |
| 808 | 3149508743 | Power N-CT41^2T14S13 |
| 1134 | 3186650232 | Power N-CT41^2T3S13 |
| 1198 | 3189119472 | Power N-CT41^2Arc(14) |
| 1226 | 3320353422 | Power N-CT41^2Arc(13) |
| 1370 | 3379875120 | Power N-CT37^2+1 |
| 1372 | 3416913720 | Power N-CT37^2+3 |
| 1373 | 3885939702 | Add 1 factors |
| 1381 | 3976523172 | Power N-CT41^2Arc(8) |
| 1415 | 4107757122 | Power N-CT41^2Arc(7) |
| 1450 | 4238991072 | Power N-CT41^2Arc(6) |
| 1486 | 4370225022 | Power N-CT41^2Arc(5) |
| 1523 | 4501458972 | Power N-CT41^2Arc(4) |
| 1561 | 4632692922 | Power N-CT41^2Arc(3) |
| 1600 | 4763926872 | Power N-CT41^2T1T1 |
| 1640 | 4895160822 | Power N-CT41^2T1 |
| 1681 | 5026394772 | Power N-CT41^2 |
| 1682 | 5495420754 | Add 1 factors |
| 1683 | 5709003516 | Add 2 factors |
| 1720 | 5732162195 | Power N-CT43^2T3 |
| 1722 | 5863396002 | Power N-CT43^2T2T1 |
| 1763 | 5863396145 | Power N-CT43^2T2 |
| 1764 | 5927780580 | Power N-CT43^2T1T1 |
| 1806 | 5927780723 | Power N-CT43^2T1 |
| 1851 | 5927780866 | Power N-CT43^2+2 |
| 1880 | 6343756542 | Power N-CT47^2T7 |
| 1939 | 6445283775 | Power N-CT47^2Trin2,2,2 |
| 8000 | 6450237864 | Power CT31^3T11T11T11 |
| 8400 | 6494677325 | Power CT31^3T11T11T10 |
| 8820 | 6539116786 | Power CT31^3T11T10T10 |
| 9600 | 6551227864 | Power CT31^3T11T11T7 |
| 10000 | 6591375450 | Power CT31^3T11T11T6 |
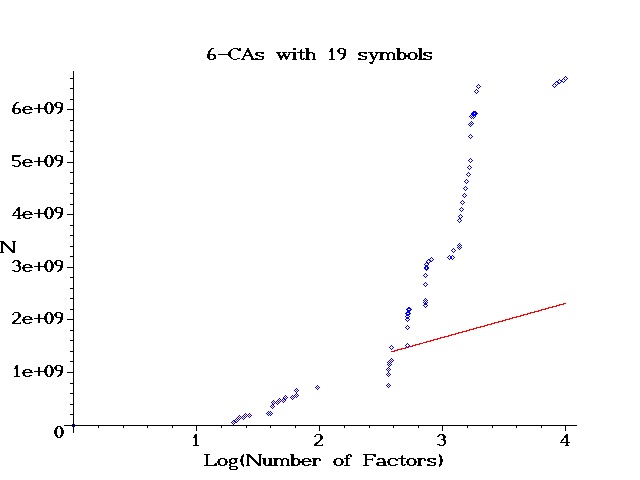
| | Graph:
 |
