| k | N | Source |
| 26 | 244140625 | orthogonal array |
| 28 | 387420485 | orthogonal array fuse fuse |
| 30 | 594823313 | orthogonal array fuse fuse fuse fuse |
| 32 | 887503669 | orthogonal array fuse fuse fuse fuse fuse fuse |
| 35 | 976562425 | perfect hash family4,35,25,c |
| 50 | 1181640625 | double OA (Colbourn-Zhou) |
| 52 | 1191390625 | double OA (Colbourn-Zhou) |
| 53 | 1615567282 | Martirosyan-TVT variant |
| 56 | 1883263604 | Martirosyan-TVT |
| 57 | 2441406240 | perfect hash family10,57,26 |
| 65 | 2685546625 | perfect hash family11,65,25,c |
| 66 | 2685546864 | perfect hash family11,66,26 |
| 69 | 2929687225 | perfect hash family12,69,25,c |
| 72 | 2929687488 | perfect hash family12,72,26 |
| 75 | 3237001225 | Add 25 factors |
| 76 | 3246751225 | Add 25 factors |
| 77 | 3270001225 | Add 25 factors |
| 80 | 3417968736 | perfect hash family14,80,26 |
| 125 | 3662109025 | perfect hash family15,125,25,c |
| 625 | 3906249625 | perfect hash family16,625,25,c |
| 626 | 3906249984 | Power CT25^2+1 |
| 627 | 5049624984 | Add 1 factors |
| 628 | 5518359984 | Add 2 factors |
| 651 | 5768888164 | Power CT27^2Arc(3) |
| 676 | 5912168024 | Power CT27^2T1T1 |
| 702 | 6055447884 | Power CT27^2T1 |
| 730 | 6198727744 | Power CT27^2+1 |
| 731 | 7756011544 | Add 1 factors |
| 757 | 8300141196 | Power N-CT29^2Arc(3) |
| 784 | 8507544024 | Power N-CT29^2T1T1 |
| 812 | 8714946852 | Power N-CT29^2T1 |
| 842 | 8922349680 | Power N-CT29^2+1 |
| 843 | 10749710280 | Add 1 factors |
| 844 | 11481245280 | Add 2 factors |
| 1064 | 11895280636 | Martirosyan-TVT |
| 1250 | 12129649876 | Martirosyan-TVT |
| 1251 | 12221530971 | Martirosyan-TVT variant |
| 1252 | 12313405971 | Martirosyan-TVT |
| 1254 | 13906766571 | Martirosyan-TVT |
| 1256 | 14805505347 | Martirosyan-TVT |
| 1300 | 15056033527 | Martirosyan-TVT |
| 1301 | 15174634352 | Martirosyan-TVT variant |
| 1302 | 15293235177 | Martirosyan-TVT |
| 1316 | 15748748596 | Power N-CT47^2T19 |
| 1410 | 15956151424 | Power N-CT47^2T17 |
| 1504 | 16248831780 | Power N-CT47^2T15 |
| 1645 | 16337890536 | Power N-CT47^2T12 |
| 2212 | 16542968736 | Power N-CT47^2+3 |
| 2239 | 17527822050 | Power N-CT53^2Arc(12) |
| 2281 | 17951998707 | Power N-CT53^2Arc(11) |
| 9351 | 18088839984 | Power CT31^3T5S30 |
| 10000 | 18232119844 | Power CT31^3T3S30 |
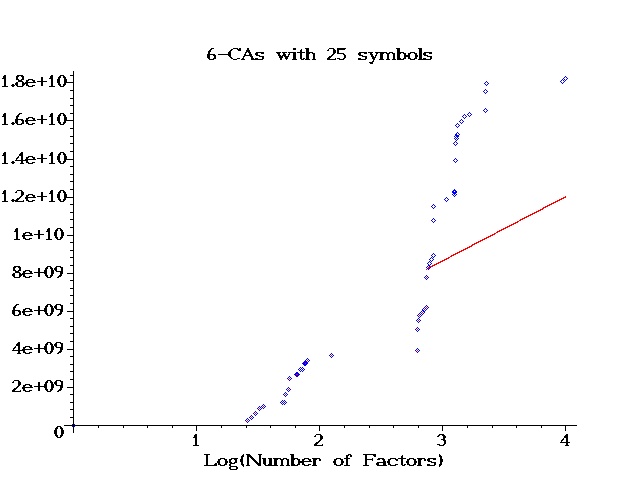
| | Graph:
 |
