| k | N | Source |
| 6 | 32 | orthogonal array |
| 7 | 42 | Special (Yan Jun) |
| 8 | 52 | Steiner system (CKRS) |
| 9 | 54 | Steiner system (CKRS) |
| 10 | 56 | Steiner system (CKRS) |
| 14 | 64 | cross-sum (CKRS) |
| 15 | 79 | simulated annealing (Torres-Jimenez) |
| 16 | 98 | SBSTT (TJ-AG) |
| 20 | 99 | SBSTT (TJ-AG) |
| 21 | 109 | SBSTT (TJ-AG) |
| 22 | 111 | SBSTT (TJ-AG) |
| 23 | 114 | SBSTT (TJ-AG) |
| 24 | 117 | SBSTT (TJ-AG) |
| 25 | 118 | SBSTT (TJ-AG) |
| 26 | 130 | SBSTT (TJ-AG) |
| 35 | 134 | Cyclic (Colbourn-Keri) |
| 68 | 136 | Paley type (Colbourn) |
| 72 | 144 | Paley type (Colbourn) |
| 80 | 159 | SBSTT (TJ-AG) |
| 84 | 168 | Paley type (Colbourn) |
| 90 | 178 | Paley type (Colbourn) |
| 98 | 194 | Paley type (Colbourn) |
| 102 | 202 | Paley type (Colbourn) |
| 103 | 206 | Paley type (Colbourn) |
| 104 | 208 | Paley type (Colbourn) |
| 108 | 214 | Paley type (Colbourn) |
| 110 | 218 | Paley type (Colbourn) |
| 114 | 225 | SBSTT (TJ-AG) |
| 122 | 241 | SBSTT (TJ-AG) |
| 128 | 252 | Paley type (Colbourn) |
| 132 | 260 | Paley type (Colbourn) |
| 138 | 271 | SBSTT (TJ-AG) |
| 140 | 273 | SBSTT (TJ-AG) |
| 143 | 288 | SBSTT (TJ-AG) |
| 150 | 289 | SBSTT (TJ-AG) |
| 152 | 292 | SBSTT (TJ-AG) |
| 155 | 303 | SBSTT (TJ-AG) |
| 158 | 304 | SBSTT (TJ-AG) |
| 164 | 310 | SBSTT (TJ-AG) |
| 168 | 318 | SBSTT (TJ-AG) |
| 170 | 322 | SBSTT (TJ-AG) |
| 174 | 327 | SBSTT (TJ-AG) |
| 180 | 332 | SBSTT (TJ-AG) |
| 192 | 346 | SBSTT (TJ-AG) |
| 194 | 357 | SBSTT (TJ-AG) |
| 359 | 359 | Cyclic, derived (Colbourn-Keri) |
| 378 | 379 | Cyclic, derived (Colbourn-Keri) |
| 379 | 380 | Paley type (Colbourn) |
| 431 | 430 | Paley type (Colbourn) |
| 433 | 434 | Cyclotomy (Colbourn) |
| 463 | 462 | Paley type (Colbourn) |
| 467 | 466 | Paley type (Colbourn) |
| 487 | 486 | Paley type (Colbourn) |
| 491 | 490 | Paley type (Colbourn) |
| 499 | 498 | Paley type (Colbourn) |
| 503 | 503 | Cyclic, derived (Colbourn-Keri) |
| 509 | 509 | Cyclic, derived (Colbourn-Keri) |
| 521 | 521 | Cyclic, derived (Colbourn-Keri) |
| 523 | 523 | Cyclotomy (Colbourn) |
| 541 | 541 | Cyclotomy (Colbourn) |
| 547 | 547 | Cyclotomy (Colbourn) |
| 557 | 557 | Cyclotomy (Colbourn) |
| 563 | 563 | Cyclotomy (Colbourn) |
| 569 | 570 | Cyclotomy (Colbourn) |
| 571 | 571 | Cyclotomy (Colbourn) |
| 577 | 577 | Cyclotomy (Colbourn) |
| 587 | 587 | Cyclotomy (Colbourn) |
| 593 | 593 | Cyclotomy (Colbourn) |
| 599 | 599 | Cyclotomy (Colbourn) |
| 601 | 601 | Cyclotomy (Colbourn) |
| 607 | 607 | Cyclotomy (Colbourn) |
| 613 | 613 | Cyclotomy (Colbourn) |
| 1230 | 615 | Derive from strength 6 |
| 1282 | 641 | Derive from strength 6 |
| 1318 | 659 | Derive from strength 6 |
| 1360 | 680 | Derive from strength 6 |
| 1366 | 683 | Derive from strength 6 |
| 1372 | 686 | Derive from strength 6 |
| 1380 | 690 | Derive from strength 6 |
| 1422 | 711 | Derive from strength 6 |
| 1426 | 713 | Derive from strength 6 |
| 1428 | 714 | Derive from strength 6 |
| 1438 | 719 | Derive from strength 6 |
| 1446 | 723 | Derive from strength 6 |
| 1458 | 729 | Derive from strength 6 |
| 1482 | 741 | Derive from strength 6 |
| 1486 | 743 | Derive from strength 6 |
| 1492 | 746 | Derive from strength 6 |
| 1498 | 749 | Derive from strength 6 |
| 1510 | 755 | Derive from strength 6 |
| 1522 | 761 | Derive from strength 6 |
| 1548 | 774 | Derive from strength 6 |
| 1558 | 779 | Derive from strength 6 |
| 1566 | 783 | Derive from strength 6 |
| 1570 | 785 | Derive from strength 6 |
| 1578 | 789 | Derive from strength 6 |
| 1582 | 791 | Derive from strength 6 |
| 1690 | 792 | Power CZ3-13.12-10.1 |
| 1859 | 814 | Power CZ3-13.12-11.1 |
| 2198 | 819 | Power CT13^3+1 |
| 2380 | 938 | Power CT68^2,cT33c |
| 4624 | 940 | Power CT68^2,c |
| 4707 | 986 | Power CT73^2Arc(7)T2 |
| 4896 | 988 | Power CT72^2,cT4c |
| 5184 | 996 | Power CT72^2,c |
| 5440 | 1078 | Power CT80^2,cT12c |
| 5760 | 1086 | Power CT80^2,cT8c |
| 5867 | 1097 | Power CT81^2Arc(7)T2 |
| 6400 | 1101 | Power CT80^2,c |
| 6720 | 1155 | Power CT84^2,cT4c |
| 7056 | 1164 | Power CT84^2,c |
| 7200 | 1215 | Power CT90^2,cT10c |
| 7560 | 1224 | Power CT90^2,cT6c |
| 8100 | 1234 | Power CT90^2,c |
| 8232 | 1320 | Power CT98^2,cT14c |
| 8820 | 1330 | Power CT98^2,cT8c |
| 9604 | 1346 | Power CT98^2,c |
| 9898 | 1394 | Power CT101^2,cT3c |
| 10000 | 1402 | Power CT100^2,c |
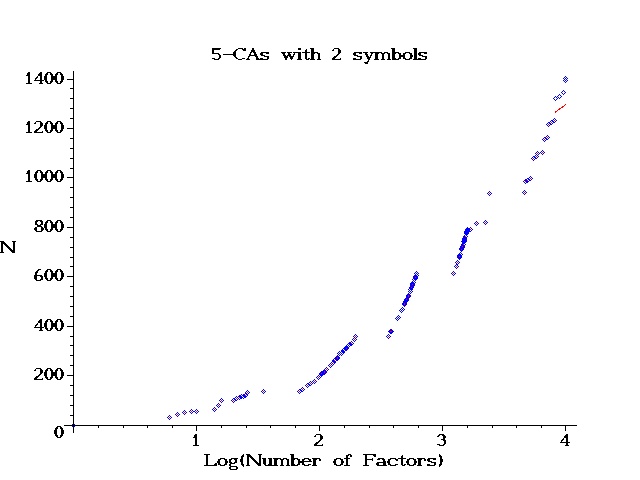
| | Graph:
 |
