| k | N | Source |
| 26 | 9765625 | orthogonal array |
| 28 | 14348903 | orthogonal array fuse fuse |
| 30 | 20511141 | orthogonal array fuse fuse fuse fuse |
| 32 | 28629139 | orthogonal array fuse fuse fuse fuse fuse fuse |
| 33 | 29296825 | perfect hash family3,33,25,c |
| 34 | 29296872 | perfect hash family3,34,26 |
| 52 | 38671875 | Martirosyan-TVT |
| 53 | 49168391 | Martirosyan-TVT variant |
| 56 | 55401793 | Martirosyan-TVT |
| 68 | 58593744 | perfect hash family6,81,27S6 |
| 70 | 63177022 | perfect hash family6,81,27S5 |
| 72 | 67760300 | perfect hash family6,81,27S4 |
| 74 | 72343578 | perfect hash family6,81,27S3 |
| 76 | 76926856 | perfect hash family6,81,27S2 |
| 81 | 78124825 | perfect hash family8,81,25,c |
| 82 | 78124992 | perfect hash family8,82,26 |
| 103 | 87890425 | perfect hash family9,103,25,c |
| 104 | 87890616 | perfect hash family9,104,26 |
| 114 | 97656025 | perfect hash family10,114,25,c |
| 532 | 97656240 | Power N-CT23^2+3 |
| 625 | 107421625 | perfect hash family11,625,25,c |
| 626 | 107421864 | Power CT25^2+1 |
| 627 | 126171264 | Add 1 factors |
| 651 | 144088088 | Power CT27^2Arc(3) |
| 676 | 148671366 | Power CT27^2T1T1 |
| 702 | 153254644 | Power CT27^2T1 |
| 730 | 157837922 | Power CT27^2+1 |
| 731 | 180462448 | Power N-CT29^2Arc(4) |
| 757 | 186624686 | Power N-CT29^2Arc(3) |
| 784 | 192786924 | Power N-CT29^2T1T1 |
| 2500 | 195312480 | Power CT25^3Tlev |
| 10000 | 205077625 | perfect hash family21,15625,25,c |
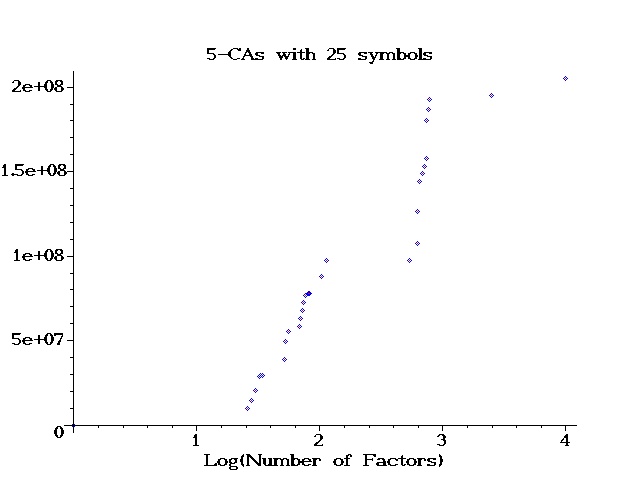
| | Graph:
 |
