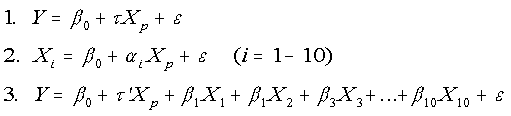
I have been asked to perform a mediational analysis on data from a study which tests the effect of a school-based intervention on fruit and vegetable consumption in grade school children. Ten possible mediators have been selected for testing in the model. I have used the regression method discussed in your 1994 paper, "Analysis of Mediating Variables in Prevention and Intervention Research" extended to more than one mediator and a random effects model as described by W.B. Hansen & R.B. McNeal in "How D.A.R.E. Works: An Examination of Program Effects on Mediating Variables", 1997, Health Education and Behavior, Vol. 24 (2): 165-176.
As your paper describes, I performed regression analyses of three types as shown below:
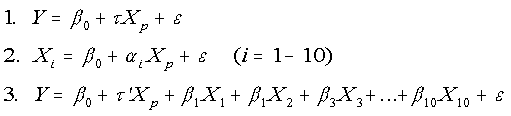
In my analysis, (2) is tested by regressing each of the possible mediators on the program, (3) is tested by regressing the outcome (consumption) on intervention and all possible mediators. I found only one mediator which was significant in (2) and (3).
My question to you is: in a multi-mediator model, how is the proportion of the mediated effect determined? In my example, for which the 3rd mediator was significant (i.e. X3), my instinct is to calculate the proportion as:
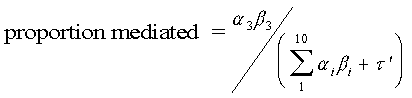
Is this correct? My concern is that, in my
example, for several of the non-significant mediators, the a is positive
in sign while the b is negative. I'm not sure how to interpret this;
I don't know if it makes sense that these mediators contribute "negatively"
to the total mediated effect. Another possibility is to calculate
b3 from a regression equation which includes only the mediator
#3 and the intervention variable. This brings up another question: when
I tried this I found that 
(.0454 vs. .0538). Do you know why this would be the case?
Your response to my questions would be greatly appreciated. Since I am a novice in the field of mediational analysis, any references that you could recommend to me would also be very helpful.
I had calculated the % mediated for my significant mediator (which was self efficacy, by the way) several different ways and found that it varied just slightly across methods. By using the absolute value of all indirect effects, I got 4.2% (total effect=.973). Treating the negative indirect effects as zero, I got 4.4% (total effect=.927). Treating them as negative, I got 4.6% (total effect=.881). I also calculated the percent using tau as the total effect (from the regression of outcome on intervention alone). In this case, the total effect was .935 and the % mediated was 4.3%. What do you think about using tau for the total effect in the denominator? As you can see, self-efficacy is a pretty weak mediator. The intervention effect remained highly significant when modeled along with the mediators.
Thank-you for your time,
Julie Maloy
Dept. of Biostatistics
AMC Cancer Research Center
Denver, CO
An Answer to Julie's Question from Dr. David MacKinnon
Hello Julie,
Thanks for your questions. Sounds like you have a very interesting study.
Starting with
;
this is usually because the sample size is different in the models used
to estimate mediated effects. Assume that the independent variable
and the mediating variable are available from 200 cases and the dependent
variable is present for 160 cases, i.e., 40 cases are missing the dependent
variable. The a parameter will
be based on a regression with 200 cases and the b
will be based on 160 cases. The t and
t'
parameters will be based on 160 cases. To get t
- t' = ab the same
subjects and the same sample size must be used to estimate all of the parameters.
In other regression analysis such as logistic regression and multilevel
models
but in the case of ordinary regression it does. As a result
the total effect measured by t should exactly
equal the total effect measured by t' +
ab. I hope this solves this discrepancy.
The problem with the proportion mediated is common in multiple mediator models. Some mediated effects will have different signs. Whenever this happens the total effect is ambiguous and it is possible to have -% which does not make sense. For example, lets say that the total effect is zero, then the percent mediated is undefined even though there could be large mediated effects, although in opposite directions. One solution is to take the absolute value of all the indirect effects and the direct effect and call that the total effect and then divide each effect by this new total effect. If the inconsistent mediation effects (with opposite signs) are not too large I think this still gives a reasonable look at the model. Another strategy is to include only significant paths. If you are lucky, then all of these mediated effects and the direct effect will have the same sign.
Mediators that contribute negatively--counterproductive processes-- were not present in my earlier analysis of a gateway drug (cigarettes, alcohol, and marijuana) prevention program although there was nonsignificant evidence that increases in communication skills, a mediator targeted by the program, tended to give such counterproductive effects, i.e. increased rather than decreased drug use. I have several counterproductive mediated effects in the analysis of an anabolic steroid prevention program. For example, football players who received the program learned more about the positive consequences of steroid use and students who knew more about the positive consequences were more likely to intend to use steroids - a counterproductive mediation effect. Fortunately, other mediational processes were in the right direction leading to an overall significant beneficial effect. These types of effects, if they are interpretable, could be used to improve the program. It looks like teaching players the positive effects of steroids backfired so maybe the next version of the program will not teach as many positive effects of anabolic steroid use.
Which mediator was the most important one?
Some useful references
Alwin, D. F. and Hauser, R. M. (1975). The decomposition of effects in path analysis. American Sociological Review, 40(February), 37-47. See the footnote #3 on page 43 where it is stated that taking absolute values of all effects prior to computing percentage mediated may help understand effects in models with positive and negative mediated effects.
Davis, J. A. (1985). The logic of causal order. SAGE Quantitative Psychology Series Paper 55. Newbury Park, CA. See pages 56-58 for discussion of multiple mediator models with some mediated effects with opposite signs.
MacKinnon, D. P. (2000). Contrasts in multiple mediator models. In J. Rose, L. Chassin, C. C. Presson, & S. J. Sherman (Eds.), Multivariate applications in substance use research: New methods for new questions (pp. 141-160). Mahwah, NJ: Erlbaum.
MacKinnon, D. P., *Krull, J. L., & *Lockwood, C. M. (2000). Equivalence of the mediation, confounding, and suppression effect. Prevention Science, 1 (4), 173-181 .
I am now working on measures of effect size in multiple mediator models. It is possible that there will be some alternative measure that will incorporate consistent and inconsistent mediation (suppressor) effects.
Let me know what you think.
Regards,
Dave MacKinnon
An Answer to Julie's Question from Dr. David Kenny
Dear Julie (if I may),
Ignoring sampling error I would think that the answer to your question is
for mediator I would be
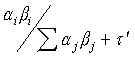
it is very possible that one or more variables might be a 'negative' mediator, but you should treat it as such.
and the total mediation would be
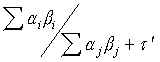
of course, you may wish to trim one or more mediators from the equation based on significance testing. If that is done, the above formulas still apply.
I hope this helps, Dave K.
David A. Kenny
Department of Psychology U-20
University of Connecticut
Storrs, CT 06269-1020
FAX (860) 486-2760 Homepage:http://nw3.nai.net/~dakenny/kenny.htm