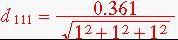ECE 350 Homework Set #6

Solutions

Due Monday Sept. 14

1. Copper has FCC crystal structure with lattice parameter 0.361nm. Calculate the interplanar spacing for the following planes: (111), (220),(100).

Answer: 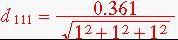=.208nm

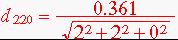= 0.128nm

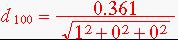= 0.361nm

2. Calculate the planar density of atoms on each of the planes in problem 1. (Use units of atoms/nm².)

Answer: The (111) in the unit cube is an equilateral triangle whose area is 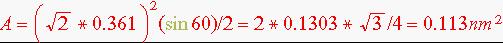This area contains two atoms since the 3 atoms in the centers of the edges are each shared between two triangles and the 3 corner atoms are each shared between 6 triangles. Thus the areal density of atoms is 2/0.113 = 17.72 atoms/nm².

The 220 plane section in the unit cell is a rectangle with sides = a and its area is 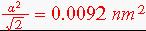. The areal density of atoms on this plane is 1/0.0092 = 10.85 atoms/nm².

The (100) plane section is a square with area a² and it has 2 atoms in this area so areal density of atoms is 2/0.361² = 15.34 atoms/nm².

3. Calculate the volume density of atoms for each set of planes and intraplanar spacings calculated in problems 1 and 2.(Use units of atoms/nm³).

Answer: The volume density of atoms = (areal density)/d_hkl so for (111) atoms/nm³ = 17.72/.208 =85

(220) atoms/nm³ = 10.85/.128 = 85

(100) atoms/nm³ = 15.34/.361 = 42.5

Note the last value is only 1/2 the previous two values because there is an equivalent set of parallel planes with half the lattice spacing of the (100) also if we calculate the volume density of the unit cell as 4 atoms/a³ = 4/(0.361)³ = 85 atoms/nm³.

Return to Syllabus

Return to ECE 350 Page