Chapter 8 notes

Applications of Chemical Dynamics

Enzyme Kinetics

 Hemoglobin, transcription regulation and enzyme kinetic are examples of linked equilibria. Here, we will just couple the linked equilibrium to the kinetics of enzyme reactions. These types of problems, and related ones involving steady state concentrations of species, come up over and over again in biochemistry. We did this in a simple way linking transcription systems together. Most of you have seen some of the equations from enzyme kinetics before. Let’s start with the interactions between the substrate and the enzyme and then various models for how different kinds of affector molecules can regulate the substrate enzyme interaction. To a large extent, this is how the control of metabolic rates and pathways is achieved in your bodies and in all other living organisms.

Consider some general reaction which is catalyzed by an enzyme:

Let Ks be the dissociation constant for the interaction between the enzyme and substrate and lets assume for now that this equilibrium is achieved quickly on the timescale of the reaction (we consider the kinetic part of enzyme kinetics later). The rate of the reaction is of course just given by:

Here the derivative of P with respect to time is what we normally call the velocity in an enzymatic reaction. As you can see, what matters is the concentration of the active species, ES. The equilibrium relationship above relates ES to S, the substrate concentration (which we know) and E, the free enzyme concentration (which we do not know). We do not know E in the free form, but we normally do know Et, the total amount of enzyme. Thus we can see that:

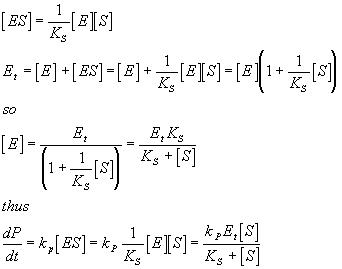
Which is an equation that you may know from other classes. Note that k_pE_t is often referred to as V_max and dP/dt is often just called V giving:

V = V_max[S]/(K_S +[S])

Which is often called the Michaelis/Menten equation

Consider the thermodynamics involved here. The thermodynamic arguments were for the calculation of the concentration of [ES] and this was linearly related to the rate or velocity of the reaction. It is generally true that what we want to do is to calculate the amount of the activated form of the enzyme and very often we will do this by assuming an equilibrium between the enzyme and the various things which associate with it such as the substrate.

So, how does this relate to affectors of enzymatic function? Well, the most common affectors in Biochemistry are those that perturb the equilibrium either in favor of or against the formation of the activated complex. Consider the case of a competitive inhibitor, where a molecule binds in place of the substrate:

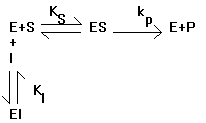
The solution for the initial velocity looks much the same as before with one extra term:

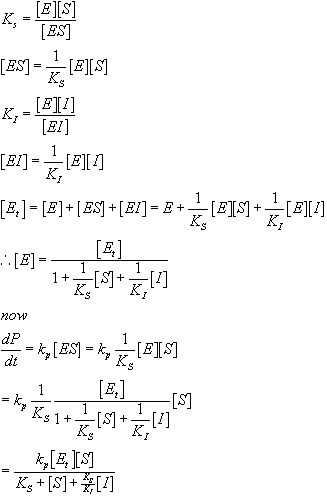
Note that this is just what you get for the no inhibitor case with one extra term in the denominator. Also note that as I increases, the rate decreases and that if you let S be at high enough concentration for any given concentration of I, the expression reduces to the same expression we had without an inhibitor present. This is why I is called a competitive inhibitor. It competes for binding with S and therefore if you add enough S you can effectively compete off all of the I. This is not true of all inhibitors, as we will discuss in class. Below, we will consider the case of a required activator, where the enzyme only works when the activator is bound.

Note that these types of interactions and control mechanisms are important not only in classical enzyme kinetics but also in the closely related subjects of transcription and translation control.

A general approach to applying linked equilibrium to simple enzyme kinetics

What follows is a general method for solving fairly complex systems of enzymes in which the substrate binding is assumed to be in equilibrium. While this is not always true, we will generalize later using a steady state assumption (this gives K_M instead of K_S for those of you the know something about enzyme kinetics). 

This method works for any system where there is a small amount of something (like an enzyme or a piece of DNA that is part of a transcription initiation complex or a protein that binds and transports a small molecule) and a much larger amount of the thing that that something binds too (like a substrate or a transcription initiation factor or oxygen which binds to hemoglobin and is transferred to the tissues). In this case, as long as binding is fast relative to any chemical reaction that may follow, we can simply write down a mathematical description of the system that can be solved to give the relative concentration of any possible bound state.

Consider the example below of an enzyme that is only active when an activator is bound. We will consider that case where binding of S and A are independent. Thus the binding of A is characterized by the dissociation constant K_Act and the dissociation constant for the substrate is characterized by K_s. The rate constant for the first order conversion of AES to product is k_p.

E+S « ES

+ +

A A

Ý Ý

ß ß

AE + S « AES ® A + E + P

First, determine what you want to know.

Usually what we want to know is how the concentration of the affector(s) in the system affects the activity of the system. The activity of this system is just the rate of formation of the product. The reaction shown is first order in AES and thus the rate of P's formation is just [AES]k_p. In other words, the activity of the system is directly proportional to the amount of activated enzyme that is present and is bound to a substrate molecule (AES). So, what we want to know is the relative concentration of AES.

Next, determine what we do know.

As long as the concentrations of A and S are much larger than E, then we do not have to worry about the concentrations of A or S changing early in the reaction. Thus, we know the concentrations of free A and S initially, because they are essentially equal to the amount that we added in the first place. In principle we also know the total amount of enzyme added to the system (but we usually do not know the amount of free or bound enzyme). So, we would like to solve for [AES] in terms of E_tot, S and A.

Write down the equilibrium relationships.

We know that:

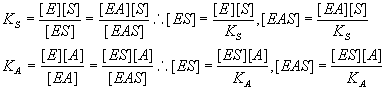
Write down the relative concentration of the active species.

Substitute the equilibrium relationships into the mass action equation.

Solve for [E].

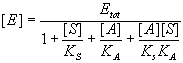
Substitute this into the equilibrium expression(s) of interest.

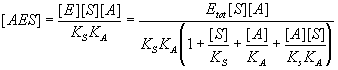
Finally, write down the expression for relative activity.

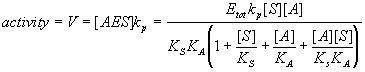
Generalizing this approach for steady state reactions:

Look back at the steady state assumption (the assumption that the intermediate, ES, is formed about as fast as it decays and therefore remains constant). Note that the only difference is that we get a steady state constant instead of an equilibrium constant. But other than that, the math is the same as for the equilibrium assumption case. We can do that here as well. Let’s assume that the active form of the enzyme is not in equilibrium but in steady state with respect to the binding of the substrate (but since A is not consumed, we will assume that binding of A is in equilibrium). The only difference is that now K_S which is the dissociation constant for S and is given by the ratio of the forward and backwards rate constants for binding of S, is replaced by K_M which is the steady state dissociation constant (the inverse of the steady state constant we discussed before) and is given by the ratio of the reverse rate constant plus k_p divided by the forward rate constant for substrate binding. In other words,

K_S = k_b/k_f

K_M = (k_b + k_p)/k_f

Where k_f and k_b are the forward and reverse rate constants for binding of the substrate (S), respectively. So you get the same equations that you do for the equilibrium model above, but you substitute K_M for K_S.

Marcus Theory of Electron Transfer (download pdf)