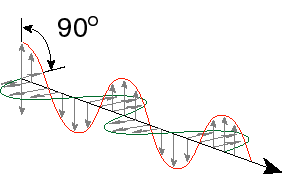
What is light? From physics class, perhaps you learned that light is an electromagnetic wave. I won't go through all the derivations from Maxwell’s equations and such, but it is easy to demonstrate that changing electric fields give rise to changing magnetic fields and changing magnetic fields give rise to changing electric fields. Thus, you can set up an oscillator that alternates between a magnetic field and an electric field. You can show that such an oscillation will propagate though space as it goes back and forth between the magnetic and electric fields. Thus one of the properties of light is that it has a particular speed. This speed depends on what material the light is traveling through, but in a vacuum the speed of light is 2.988 x 108 m/s. Since light is nothing more than exchange between an electric and magnetic field, it is a form of pure energy (no mass). Because light is an oscillating field, it has a frequency of oscillation. Because it is traveling through space at a constant speed, the light will cover a certain distance within one oscillatory cycle. This is called the wavelength of light. Finally, it turns out that the amount of energy in wave of light is proportional to its frequency – the higher the frequency of light, the higher the energy. High frequency also corresponds to a short wavelength, so wavelength and frequency are inversely related. Let’s write down some of this:
E = hn
n = c/l
E = hc/l
E is energy. The number h is called Planck’s constant and has the value 6.626 x 10-34 J s. The constant c is the speed of light, n is the frequency of oscillation of light, and l is the wavelength of light. An illustration of some of these principles is below.

Here, the peak to peak distance is called the wavelength, the number of times that the light wave oscillates per second is the frequency in Hz and the two waves perpendicular to one another but 90 degrees out of phase are the electric field and the magnetic field.
Now light can have almost any energy. Low energy light we know of as radio waves – electromagnetic radiation that travels through space between your radio and the radio station. The frequencies for this type of radiation are on the order of MHz (106 Hz or millions of times per second – Hz stands for hertz which is the number of times something repeats per second) to hundreds of megahertz. Up in the gigahertz range (billions of oscillations per second) is the microwave region. At somewhat higher frequencies we have infrared light (roughly a frequency of 1014 Hz), then visible red light, visible orange, yellow, green blue violet (on the order of 1015 Hz) and then the ultraviolet spectrum. At higher frequencies yet, there are X-rays (1017 Hz), gamma-rays and other very high energy photons.
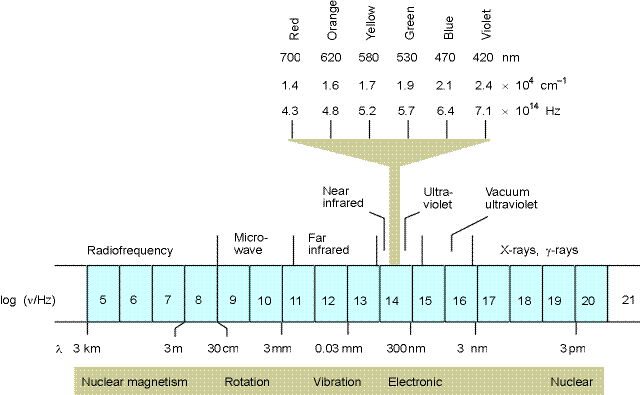
Fig. 16.1 from Physical Chemistry by Atkins
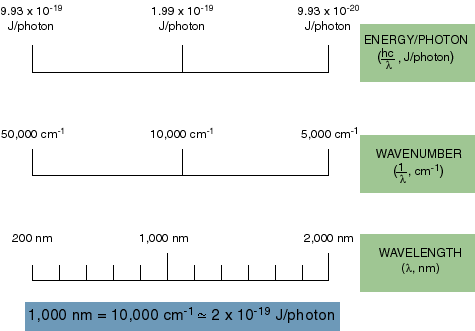
How about units? We talk about light energy in joules sometimes, but more often we use the wavelength of light to designate its energy or the inverse of the wavelength in centimeters (called inverse centimeters or wavenumbers).
We are now ready to explore the question, why is light colored. Easy, you say, because it has a particular energy. OK, but the energy of what, per what? If light is just a continuous wave, its energy depends on its frequency, sure, but we should be able to get the same amount of energy from low frequency light as from high frequency light by increasing the amplitude of the wave (the size of the oscillating field). This should mean that we can trade amplitude and frequency against each other and maintain a constant energy. Thus, if I have a high enough amplitude of visible light, it should act like an X-ray. But is does not. It’s properties of interaction with matter depend strictly on the frequency of light and not on the amplitude (at least up to a point). It is as though light comes in packets of a set amplitude and the only thing you can vary is the frequency.
These days it is possible to build extremely sensitive detectors of light. If you turn the light level lower and lower and shine it on one of these detectors, you find that instead of a just seeing the amplitude of light decrease uniformly, you eventually get to a point where one sees individual spikes on the detector and then nothing in-between. These spikes are single packets of light which are called photons. Photons have only one property, frequency. This determines their energy (color). Thus, the fact that light comes in packets is intimately related to the fact that it has a distinct color. It is the energy per packet (the frequency of the oscillation in the packet) that determines the color.
The quantum nature of matter. Next, we need to consider why matter would interact with one energy (color) of photon and not another. To understand this, we need to remember that what a photon is is an oscillating electric and magnetic field. It turns out that the interaction of the magnetic field with matter is for the most part very weak, but the interaction of the electric field with matter is strong. Why? Well, what is matter but a bunch of negative charges (electrons) and positive charges (protons) all together. It is a pretty good bet that all these charges are likely to do something in the presence of an electric field. The question is what? How does a collection of negative and positive charges interact with an oscillating electric field? First off, it is the electrons that are likely to do the most simply because they are the lightest. Thus, they will most readily move in the presence of the field. They will try and move somehow back and forth, if you like, (though as we will see, thinking of an electron as being in one place is not perhaps the best model) as the field oscillates. In doing so they will pick up the energy from the field. But electrons in atoms or molecules are not free to move just anywhere. They are tied to nuclei by charge interactions that are very strong. Thus, they are more like balls on a spring or a rubber band. But what happens if you put a ball on a spring or a rubber band? Can you make it oscillate at any random frequency? No, a spring or a rubber band has a characteristic frequency or set of frequencies called resonance frequencies. The spring can only effectively collect energy at this frequency and its harmonics (double, triple, etc.) and not at intermediate frequencies. The forces that hold electrons near nuclei have similar characteristics. There are only certain resonant frequencies of energy that they can absorb.

So, a big part of the answer to our original question (and the basis for the electronic structure of matter) is that matter has color because the atoms and molecules that make it up contain electrons that are held to nuclei by forces, like the force of a spring or rubber band, which have particular resonance frequencies (or energies). Only certain colors of light can cause the electron to pick up (absorb energy). Since light itself comes in packets, the molecule or atom must pick up all the energy from one photon.
OK, but wait a minute. Doesn’t this really just mean that there must be at least that much energy in the photon? If there is too much, some of it just won’t get used by the transition. But that does not work. There is no where for the extra energy to go. Since energy must be conserved, absorption of a photon is an all or none event.
Matter is colored because the interactions between electrons and nuclei put constants on the space that the electron can occupy. Those constraints are like a spring or a rubber band, allowing the electron to move over a region, but only accepting oscillation energy at certain frequencies (like a spring oscillating). There are lots of examples in everyday life of energy going into matter only at certain frequencies. Consider standing waves on a spring or in a tub of water. Or how about the sound produced from instruments – again particular tones are just vibrations that happen to oscillate at a frequency that resonates with the mechanical attributes of the instruments.

It perhaps should not be so surprising that atoms and molecules have similar properties. That’s OK for light, but how about heat? I can generally heat a block of iron to whatever temperature (and thus kinetic energy) that I want. Why is it different from light energy? Remember that matter we are used to is made up of many molecules. Even though the individual molecules can only absorb certain amounts of energy (this is true even for heat energy), the block as a whole absorbs the sum of all that energy which varies almost continuously. For example, if you have a molecule that can absorb some small amount of energy, e, but only exactly that much, a million molecules together could absorb 1e or 2e or 3e or… 999,999e or 1,000,000e. Now it is pretty hard to see the difference between absorbing 999,999e and 1,000,000e. Remember that the block of metal probably has about 1023 molecules in it. This gives rise to a very continuous looking energy absorption scale in terms of total energy at heat. Light absorption is different, however, because light comes in definite chunks and travels through space without any carrier. One photon of light must be absorbed by one molecule. Thus, it does not matter how many molecules there are. If the photon has the wrong energy, it can’t be absorbed by a molecule. Heat travels from molecule to molecule by collision and can take many forms: vibration, rotation and translation. This provides many possible energy levels and methods of heat transfer.
Ok, so one clue about the structure of atoms and molecules that the early quantum mechanics had to go on was that light behaved as if it came in packets and molecules could only absorb the certain light energies just as many things on our scale preferentially absorb certain resonance energies. This, in turn implied that electrons associated with atoms and molecules had certain resonance frequencies or resonant energies. Early on, people thought about these resonant energies in terms of particles orbiting around a planet. The concept came form the concern that the electron would simply crash into the nucleus if it was not orbiting as a planet does. To this day we still refer to the resonant energies of electrons as orbitals, even though the concept of an electron orbiting a nucleus is no longer believed. This overall picture of electrons existing only in certain energy states (orbitals) is often referred to as the quantum nature of chemistry and is the basis of the periodic table of the elements and most of our modern picture of how atoms or molecules interact with one another.
This business of why electrons do not crash into the nucleus comes about from the realization that electrons are not really localized hard little balls. In fact, what has been found, is that electrons have wave-like properties. For example, they diffract (undergo positive and negative interference with each other) which is a property of waves not particles. For the lowest energy level in the hydrogen atom, for example, the electron’s distribution is, in fact, centered on the proton nucleus. However, the wavefunction of the electron (the description of the electron’s spatial distribution as a wave-like entity) extends over a region much larger than the nucleus. De Broglie formalized this wave nature of matter in the following equation (chapter 11.2):
![]()
where l is the effective wavelength, h is Plank’s constant and p is the momentum of the particle of matter.
The wave-like nature of matter and light gives rise to another phenomena that is closely related to the argument above. Since electrons (or photons or anything to some extent) do not really have a completely particle description, there is a certain difficulty in saying just where they are, how fast they are going, when they get somewhere and what energy that they have. This uncertainty is called the Heisenberg uncertainty principle. Think about our electron in the vacinity of the atom. I could tell you with with some certainty where the average position of that electron is (because the nucleus confines it to be close by) but it would be very difficult to tell you exactly what its velocity was. Likewise, if I shot the electron across the room and measured how long it took to get from one place to another, I could give you a pretty good picture of how much momentum it had, but could not really say very much about exactly where the electron was. In a similar way, since energy is proportional to frequency, if I watched a photon of light for a long time I could see many cycles of the electric field and make a good determination of the energy of the photon. However, under those circumstances, it would be difficult to say exactly when it had that energy. I could make my measurements of the frequency over a smaller number of wavelengths (shorter period of time), but this would mean that I would know when I made the measurement, but would be less certain about the value of the energy that I measured. Quantitatively, this uncertainty can be stated as (chapter 11.6):
![]()
where delta p is the uncertainty in momentum (mass times velocity) and delta q is the uncertainty in the position. A similar relationship can be derived for the relationship between the uncertainty in energy and the uncertainty in time. Thus, if one knows the position very accurately, one can have little knowledge of the particle’s momentum. If one knows the momentum accurately, one can have little knowledge of the position.
The importance of boundaries.
We have still not answered the question, why is metal shiny. This is an important question simply because it demonstrates what happens to light when it comes to a boundary and, for that matter, what happens in general to wave-like phenomena at boundaries. We all know that light has substantial wave character to it. What happens when the electric field wave from a photon hits a surface of some kind? If it matches the resonant energy of the molecules at the surface it could get absorbed. If it does not, there are two other possibilities. Either it passes through unaltered or it is bounced to somewhere else. So, why does light refect from things and why does it reflect so much better from metals than almost anything else? Metals are made in such a way that there are electrons available in what are called conduction bands. These electrons can move freely anywhere very, very fast. Thus, when they feel the electric field from the light they simple move until that field at the surface is canceled by the field of the electron charges. This is just like what happens when you tie the end of a string to a fixed point (equivalent to requiring that the electric field be zero at a particular point). If you now send a wave along that string, the wave just bounces back at you. In other words it reflects. Metals are very good at reflecting light simply because they have these electrons freely running around in conduction bands (this is also why they are good electrical conductors.
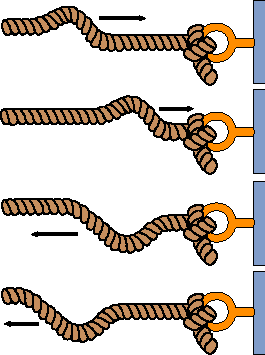
Most other substances (plastic, glass, air/liquid surfaces) do not have electrons in the conduction bands. Thus, the electric field at the surface is only partly reflected. There is some movement of electrons when the field arrives, but it does not completely cancel the field to zero. As a result, typically glass or plastic will reflect only about 5% of the light at an air/condensed phase boundary. This is enough to see your reflection in the window at night when the lights are on in the house or to see a refection of a mountain in a lake on a calm day, but no where near as much light as refects back from a shiny metal surface.
What this shows is that boundaries of substances behave like the fixed points on string. If the size of the box that the electron can move around in becomes bigger it is like having a longer string. Longer strings have lower frequencies of vibration.
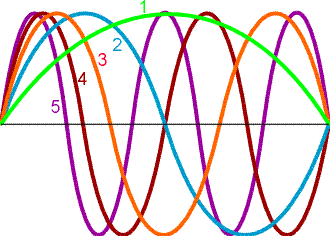
Figure 12.3 from Physical Chemistry by Atkins
So, molecules with large, long regions over which electrons can freely move will absorb light at low energy (long wavelength) and molecules with short regions where electrons can move will only be able to absorb light at high frequencies or energies. Your book discusses this principle in chapter 12.1 with the concept of a particle in a box. It goes through the solution to the Schrodinger equation for a box that allows the particle (say an electron) to move freely anywhere in the box but not through the walls of the box. Thus, the wavefunction of the particle must be zero at the edges of the box, just as is the case with our string. There are only a certain set of solutions, therefore, to the wavefunctions that work – those for which the wavefunction goes to zero at the edge of the box.
Practical Optical Spectroscopy.
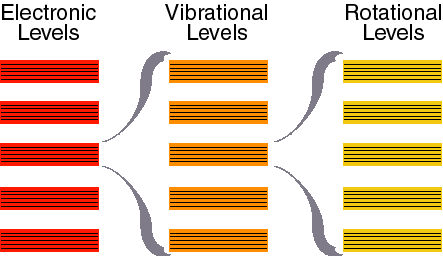
Now that we know something about the quantum nature of light and matter, we can start to consider in more detail the kinds of interactions that occur between them. It turns out that absorption of light can not only change the resonance energy of the electron itself (cause the electron to jump to a different orbital), but it can also change the movement of the nuclei in the atom or molecule by similar sorts of methods. The transition between electronic orbitals (resonance frequencies) is called an electronic transition. The transition between mechanical resonance states of the nuclei come in three flavors, vibrational transitions, rotational transitions and translational transitions (See chapter 16.1 – they do not discuss translational transition and instead consider nuclear magnetism which we shall not consider here). These are the four types of transitions that we use to explain optical spectroscopy. Electronic transitions are the highest energy and these are the ones that allow us to see and define what we call colors in the visible region of the spectrum (the total range of electronic transitions extends beyond what we can see from a few nanometers to through the ultraviolet, the visible and out to the near infrared around 1000 nm). Vibrational transitions are next in line and cause nuclei to vibrate relative to each other like balls connects by springs. These occur upon excitation in the near infrared to far infrared region of the spectrum (1000 nm to roughly 1 mm). Rotations occur in the microwave region of the spectrum (1 mm to about a meter). Translational quantum energies are very closely spaced and nearly continuous for most systems (though they can be observed for small gas molecules under special conditions). We will concentration here on electronic and vibrational spectra.

Figure 16.1 from Physical Chemistry by Atkins
Absorbance, Fluorescence, Phosphorescence and Stimulated emission
Consider a very simple electronic system consisting of two levels, the ground state (the state before absorption) and the excited state (the state after the system absorbs the photon).
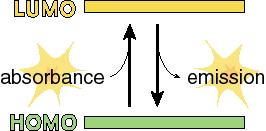
There are three types of optically detectable transitions that are possible. Light energy can be used to increase the energy of the system from the ground to the excited state. Once in the excited state, the system can come back down to the ground state either nonradiatively (without emitting a photon) or radiatively (by emitting a photon). Radiative decay of the excited state can take three forms, either spontaneous emission from the original excited state (fluorescence), spontaneous emission from a so-called triplet state after intersystem crossing (see bleow) which is called phosphorescence, or stimulated emmision.
The Nature of electronic transitions -- Let's consider the nature of electronic transitions in a bit more detail. There are three things that characterize a typical electronic transition: 1) Its wavelength (or energy), 2) Its width, 3) Its intensity.
Wavelength -- What determines the wavelength at which
a molecule absorbs light? We talked about this above in the context
of color. It is the energy spacing between electronic orbitals.
This is an important point: the absorbance spectrum in the UV/VIS/NIR
region (180 - 1500 nm) tells you about the energies of electronic
orbitals in molecules. This depends critically on structure. Many
different types of molecular systems have widely spaced electronic
orbitals and therefore absorb in the UV (high energy). This includes
the peptide bonds and the aromatic rings of proteins, the bases
of nucleic acids, and many small aromatic molecules. In the visible
and near infrared one sees transitions from large conjugated systems
(either linear, such as retinal or carotenoid, or circular, such
as chlorophylls or hemes). This is what gives rise to the colors
we see. Remember that the color you see is what the molecule does
not absorb. Thus, a red flower is absorbing blue light
and reflecting red light. In this region one can also see so-called
charge transfer transitions for coordinated metal complexes. In
the case of conjugated systems, one can use a particle-in-a-box
model and predict that the energy spacing between electronic orbitals
will depend on the size of the conjugated system: the larger their
conjugated system (corresponding to a bigger box) the lower the
energy spacing (big box, long wavelength for electronic wave function,
low energy). In general (as pointed out above), the relationship
between wavelength and energy is ![]() , where E is the
energy between levels, h is Plank’s constant (
, where E is the
energy between levels, h is Plank’s constant (![]() J sec),
c is the speed of light (
J sec),
c is the speed of light (![]() m/s), and lambda is the wavelength.
m/s), and lambda is the wavelength.
Width -- In principle, only one wavelength of light should be able to cause a transition between any two electronic states. Therefore, spectra should not have any width to them. They should simply be a series of lines representing energy differences between orbitals. However, looking at any room temperature spectrum particularly of large molecules in solution will tell you that this is not true. Spectra do have width. Why? There are three kinds of things that give rise to the width of electronic transitions:
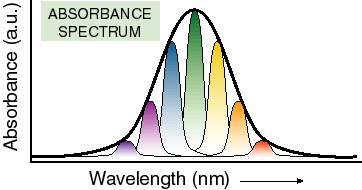
1)Changes in vibrational states which may accompany an electronic transition. This results in additional bands to the blue of the so called 0-0 transition (transition between the zero vibrational levels of the HOMO and LUMO). In large organic molecules, these vibrational bands often merge together into one wide band.
2) slower, more large-scale, nuclear motion (often in the solvent) which is coupled to (changes the energy of) the electronic transition under consideration. This generates a distribution of molecules with different spectra in the sample at any given time.
3) Something called uncertainty broadening, which is a direct consequence of the uncertainty principle of quantum mechanics. This is usually only significant compared to the other two on very simple molecules or molecules with extremely short-lived excited states.
The first two are in principle related and are easy to understand. If the nuclei of a molecule move, they may well change the energy of bonds and thus the energy of orbitals as they move. Therefore, light absorbed by a molecule can effect the energy of such movements (this is called vibrational coupling). In other words, some of the light energy absorbed goes into making the molecule move and different frequencies of movement are possible, particularly in big molecules. The second source of broadening arises when there is a distribution of nuclear positions in the population of molecules at any given time. In other words, different molecules in the sample have slightly different spectra because of the nuclear conformation they happen to have at the time of light absorption. The third source of broadening is uncertainty broadening. This is simply broadening due to the uncertainty principle (no state has an infinite lifetime and therefore there must be some uncertainty in its energy). For the most part, nuclear movement of one sort or another dominates the widths of spectra from molecules in solution.
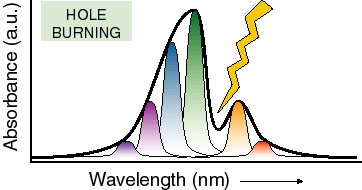
Just as an example of how nuclear motion affects absorbance spectroscopy, let’s consider the technique of hole burning spectroscopy. Here one lowers the temperature of a molecule so far that almost all nuclear motion stops (near 1 K) and then uses a laser beam at a well defined wavelength to burn a hole (bleach) all of the molecules that absorb at a particular wavelength. Since there is no nuclear motion to speak of, the conformation of these molecules, and therefore their transition energy, does not change. This results in a hole in the absorbance spectrum that has a width equivalent to what would be seen if there were no significant heterogeneity in nuclear positions in the system (this does not remove the effects of vibrations coupled to the absorption transition, just the slow conformational nuclear motions). There will also generally be holes at several energies above the energy of the lowest electronic transition which correspond to excitation of vibrations coupled to the optical transitions. By analyzing these types of spectra one can learn a great deal about specific vibrations which are associated with the absorbing cofactor.

We have a HOMO (highest occupied orbital) and a LUMO (lowest unoccupied orbital). If a photon comes along that has an energy (E = hc/l ) that matches the energy that separates the HOMO and the LUMO, then is it is possible to get transitions (move electrons) between the two orbitals. What may not immediately be obvious is that the transition can be in either direction. That is, we could either use the energy of a photon to move an electron from the lower to the upper state, or we could generate a new photon by moving the electron from the upper to the lower state.
Generating a new photon (emission) can happen in one of two ways. It can happen in exactly the same way that photons are absorbed: a photon with the right energy comes along and stimulates the transition of the electron from the upper orbital to the lower orbital. This is called stimulated emission because it only happens when a photon of the right energy comes along. The difference (the only difference) between this and absorbance is that in the case of absorbance, one photon goes into the system and no photons come out. In the case of stimulated emission, one photon goes into the system and two photons (with exactly the same phase, wavelength and direction of travel) come out. Now this can only happen when a photon interacts with a molecule in the excited state (one electron in the HOMO and one in the LUMO). Since such states are typically very short lived (billionths of a second), it can be difficult to get enough molecules into the upper state so that stimulated emission can actually be observed. This is, however, the basis of laser action, so if you put enough energy in the right place it can certainly be done.
The other way of getting emission from molecules is for a spontaneous transition to occur in which the electron collapses back down from the LUMO to the HOMO in a previously excited molecule. This is much more easily observed than stimulated emission and is called spontaneous emission or fluorescence. The study of fluorescence from biological molecules is very important because it is a very simple and fairly direct way to investigate the properties of short-lived excited states of these molecules.

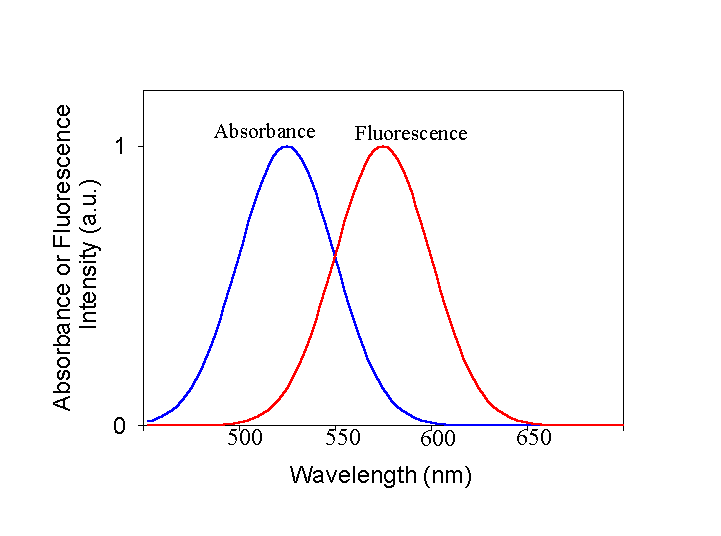
The Relationship Between Emission and Absorption Spectra. We have discussed previously what the important features of absorbance spectra are. They have a center position, they have a width and they have an intensity. The same is true for fluorescence spectra and for basically the same reasons. The energy of the emitted photon is defined by the energy difference between the initial and final states, and the spectra have width due to both nuclear movement issues and the uncertainty principle. Let's look at a representative absorbance and fluorescence spectrum of a molecule. This represents the simple case. I want you to notice two features about these spectra. First, as is essentially always the case, the peak of the fluorescence is red-shifted (at lower energy) with respect to the absorbance spectrum. Second, the fluorescence spectrum looks rather like a mirror image of the absorbance spectrum. Why?
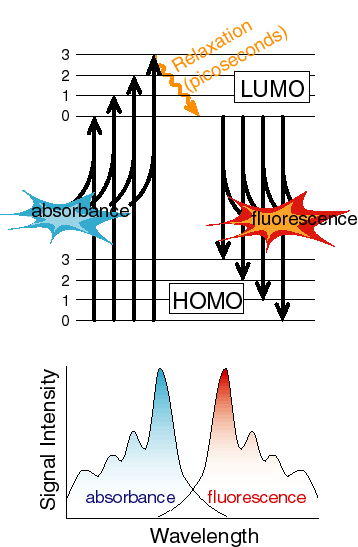
The reasons for both of these are apparent from a diagram of the electronic states and the coupled vibrational levels associated with the electronic state.

At the temperatures we work at most of the time, the majority of the molecules absorb energy from the lowest vibrational level of the ground state. However, they can often excite into any of a number of vibrational levels in the excited state. Thus, on average, the transition energy is somewhat larger than the difference between the lowest vibrational level of the ground state and the lowest vibrational level of the excited state (this difference is often referred to as the zero-zero transition energy). Exactly the opposite is true for the return trip. Any excited vibrational levels in the upper state very rapidly (picoseconds or less usually) relax to the lowest vibrational level by loosing heat to the surroundings. Now the transition that results in fluorescence occurs from the lowest vibrational level of the excited state to any of a number of vibrational levels in the ground state. On average, this transition energy is less than the zero-zero transition energy, in other words, the emitted photons are at lower energy or to the red of the absorbed photons used to generate the excited state. If the vibrational bands in the ground and excited states have the same spacing and the equilibrium nuclear configuration of the ground and excited states is the same, then the amount that the fluorescence spectrum is red-shifted from the zero-zero transition energy is the same as the amount that the absorbance spectrum is blue-shifted and the shapes of the two spectra appear to be mirror images. Note that it is not always the case that the ground and excited states have either the same equilibrium nuclear geometry or the same vibrational spacing, but the concepts described above usually hold in at least an approximate sense.
The Yield of Fluorescence. Emitting a photon is not the only way of going from an excited state to the ground state. There are other non-radiative pathways which usually involve generating heat instead of light. One can therefore ask, what fraction of the photons absorbed by a molecule result in the generation of a photon of fluorescence? This is called the quantum yield of fluorescence. We normally quantitate this concept in terms of rates. Excited electronic states are just like unstable nuclear states. They typically decay with first order kinetics. We can therefore think of the transition of the excited state to the ground state as being a competition between two first order processes, fluorescence and nonradiative decay (everything except fluorescence). The yield of fluorescence is just given by:
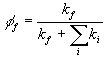
Phosphorescence. It turns out (for reasons we do not have time to go into) that there are certain types of electronic transitions which are not allowed. One such unallowed transition is a transition which involves both a change in electronic orbital and a flip of electron spin. When the spins of the two electrons in the highest orbitals are antiparallel, we refer to them as being in a singlet state. If their spins are aligned (obviously under such conditions they must be in different orbitals since you can't have two electrons with the same spin in the same orbital), we refer to them as being in a triplet state. Sometimes, the spin of an electron in the excited state will flip, usually due to interactions with the magnetic moments of the surrounding nuclei. It then forms a triplet state, and this state cannot simply undergo a direct transition to the ground state. Actually, the last statement is not quite true. Such a transition is not allowed. This is rather like your parents saying that it is not allowed to eat candy before dinner. This does not mean that it never ever happens. It just means that it is quite infrequent. Because it is so hard for a triplet state to collapse back to the ground state (which is usually singlet), the triplet state of molecules can live a long time, sometimes seconds or minutes (more often microseconds or milliseconds). When it does collapse, it can give off a photon of light and this is called phosphorescence. Molecules which do this are used in the glow-in-the-dark toys and apparel that have become popular (at least with kids the age of mine).
A Brief Description of the Measurement of Absorbance and Fluorescence.
Perhaps the most common of all analytical tools in chemistry is the UV/Vis absorbance spectrophotometer. A sketch of a simple version of such an instrument is given below:
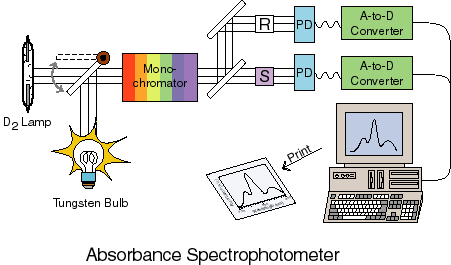
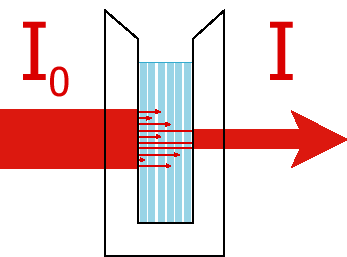
The basic idea is that some light source (usually either a UV deuterium lamp or a VIS tungsten or tungsten/halogen lamp) is used to create two equal beams of light. This light is passed through a monochromator to select a single wavelength (a monochromator uses some dispersive element such as a grating or a prism to spacially separate the colors of light and then a slit to select one of the colors). One of these beams passes through a reference sample cell which usually contains everything that is in the sample to be measured except for the molecules you want to know the spectrum of. Thus, if you are measuring bromophenol blue absorbance in an aqueous buffered solution, the reference would be an identical cell with the aqueous buffered solution by no bromophenol blue. The other beam goes through the sample cell itself. The transmittance is defined as the ratio of the intensity of light that goes through the sample cell over the intensity of light that gets through the reference cell
![]()
The absorbance or Optical Density is defined as
![]()
Note that T must be between zero and one since the amount of
light going through the sample will generally be less than the
amount going through the reference. A, therefore, will always
be a positive number. The reason for defining A in this strange
way is that, defined like this, A is directly proportional to
the concentration of the molecule in question. How does this come
about? The logarithmic dependence of transmitted light on concentration
comes from the fact that the first plane of molecules shades the
next so that each plane removes a certain fraction of the light,
![]() , when this is integrated over
all the planes, one gets the logarithmic dependence of concentration
on the intensity of transmitted light.
, when this is integrated over
all the planes, one gets the logarithmic dependence of concentration
on the intensity of transmitted light.
The relationship between concentration, absorbance and transmitted light intensity is given by the Beer-Lambert law:
![]()
where e (the Greek letter epsilon) is called the extinction coefficient and l is the pathlength of the sample cell. The extinction coefficient contains the wavelength dependence of the absorbance and is given in units of M-1cm-1. It is typical to scan the wavelength let through by the monochromator and thus get an entire absorbance spectrum, such as shown previously.
Fluorescence is measured with an emission spectophotometer as shown below:
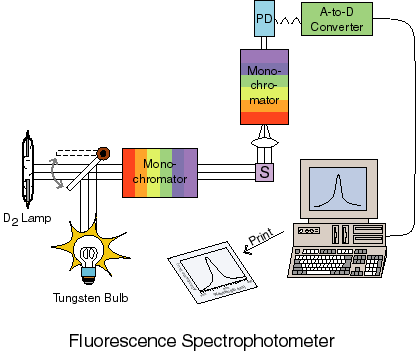
In this case there is a light source used for excitation of the sample. This light is passed through a monochromator before entering the sample. Excited molecules in the sample fluoresce as described previously and the fluorescence is collected, passed through a second monochromator (usually) and then onto a detector where the amount of fluorescence is measured.
In the case of fluorescence spectrophotometers, one typically scans the monochromator associated with the detector (though one can scan the excitation monochromator if one wants to measure the spectrum of the material absorbing the light that results in fluorescence). This results in a fluorescence spectrum, such as given above.