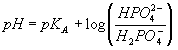
Buffer Properties
Sample Laboratory
This laboratory and its associated laboratory report are not to be performed by the student. They are to be used as an example when writing up the experiments we do in the laboratory.
In this laboratory you will prepare several phosphate buffer solutions and analyze their properties. You will start by preparing 100 mls of three buffer solutions which are 100 mM in total phosphate and have a (theoretical) pH of 7.21. 1) Prepare the first by weighing out the appropriate amount of NaH2PO4 (actually crystalized as NaH2PO4· H2O) and adding the appropriate amount of 1N NaOH (provided) and water to achieve the desired result. 2) Next prepare the buffer by mixing the appropriate amounts of NaH2PO4 and Na2HPO4 (actually crystallized as Na2HPO4· 7H2O) in water. 3) Next prepare the buffer by adding HCl to an appropriate amount of Na2HPO4 and water. Note that all of these buffers will be prepared based on the calculations that you perform below. You will not use a pH meter to titrate them to the correct pH. 4) Next, take a 10 ml aliquot of the second buffer solution and dilute it 10-fold in distilled water. 5) Next, take a 10 ml aliquot of the second buffer solution and dilute it 10-fold in 1M NaCl. Finally, perform a pH measurement on all five of the resulting buffer solutions and explain your results. Note that the pKA of the dissociation (H2PO4- <==> HPO42- + H+) is 7.21 at room temperature. The pH's of each of these solutions will probably be different and will not be exactly what you calculated. Consider the effect of activity (as opposed to concentration) in your explanation of each case.
Before coming to lab, answer the following questions. These questions will be turned in at the beginning of lab and will count for 20% of the grade for this lab.
1) How many grams of NaH2PO4· H2O and how many mls of 1N NaOH will you need to add to make the first buffer solution?
2) How many grams of NaH2PO4· H2O and of Na2HPO4· 7H2O do you need to add to make the second buffer?
3) How many grams of Na2HPO4· 7H2O and how many mls of 1N HCl will you need to add to make the third buffer?
In the Questions section of your lab report, answer the following questions.
1) What, chemically speaking, is the difference between buffer 1 and buffer 3?
2) Calculate the ionic strength of each of the solutions you made.
3) Based on your knowledge of activities and the Debye-Huckle law, do you expect the pH in buffer 4 to be greater or less than that in the original buffer 2?
4) Same as the last problem except for buffer 5.
Buffer Laboratory
Chemistry 467
Sample Prelab Report
1) How many grams of NaH2PO4· H2O and how many mls of 1N NaOH will you need to add to make the first buffer solution?
The molecular weight of NaH2PO4· H2O is 138. Our goal is to prepare a solution that is 0.1M in total phosphate (all protonated or unprotonated forms of phosphate ion). Since the only source of phosphate here is the NaH2PO4, we must add 0.1 moles per liter of this to begin with. Our final volume is 0.1 L which means we will need 0.01 moles of NaH2PO4 or 1.38 grams. This should dissociate to form Na+ and H2PO4- in solution. Considering the dissociate reaction: (H2PO4- <==> HPO42- + H+), and the relationship:
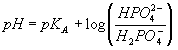
we can see that the pH will equal the pKA (7.21, or desired pH) if [H2PO4-] = [HPO42-]. In order to generate a solution in which the concentration of these two ions are equal, we will need to convert half of the diprotic phosphate to the monoprotic form by addition of a strong base, such as NaOH. Since OH- is such a strong base, the reaction will be stochiometric and therefore we will need 0.01/2 = 0.005 moles of OH- to convert half of the 0.01 moles of H2PO4- that we added above to the monoprotic form. This will require 0.005 L of the 1N NaOH solution or 5 mls. Note that we will have to be careful to leave enough volume in the cylinder upon dissolving the NaH2PO4 so that we will not go over 100 mls.
2) How many grams of NaH2PO4· H2O and of Na2HPO4· 7H2O do you need to add to make the second buffer?
As above, we find that our disired pH is achieved when the concentrations of the diprotic and monoprotic forms of the phosphate ion are equal. Thus we will want to add an equal number of moles of each to the solution. Thus, instead of adding 0.01 moles of NaH2PO4, we should add 0.005 moles each of NaH2PO4 and of Na2HPO4. That would be 0.69 grams of NaH2PO4 and 0.005 x 268 = 1.34 g of Na2HPO4.
3) How many grams of Na2HPO4· 7H2O and how many mls of 1N HCl will you need to add to make the third buffer?
This is just the opposite of the first problem. Now we need 0.01 moles of Na2HPO4 in 0.1 L of water to get a final total phosphate concentration of 0.1 M. The molecular weight of Na2HPO4 is 268. So we will need 2.68 grams. Now we need to convert half of the HPO42- to H2PO4-. This can be done by adding a strong acid like HCl. This reaction is stiochiometric. Therefore we need 0.005 moles of HCl which is 5 mls of a 1N solution.
Buffer Laboratory
Chemistry 467
Sample Laboratory Report
Procedure and Results
In this laboratory, five 100 ml phosphate buffer solutions were prepared and their pH values were measured. Solids were weighed using a Satorius analytical balance. Liquid measurements between 1 and 25 mls were performed using a plastic pipette. Liquid measurements above 25 mls were made using a graduated cylinder. The water that was used for all solutions was glass distilled water which was provided.
The first buffer solution was prepared by weighing 1.38 g of NaH2PO4· H2O (white crystalline solid) and adding this to approximately 75 mls of H2O in a 125 ml Erlenmeyer flask. To this, 5 mls of 1N NaOH (provided) was added and the solution was stirred by swirling until all of the solid had dissolved. The resulting solution was transferred to a 100 ml graduated cylinder and brought to the final volume of 100 mls by adding water and mixing.
The second buffer solution was prepared by weighing 1.34 g of Na2HPO4· 7H2O (white, crystalline solid) and 0.69g of NaH2PO4· H2O and combining them in a 125 ml Erlenmeyer flask. Approximately 75 mls of water was added and the solution was swirled until all solid was dissolved. The solution was then transferred to a 100 ml graduated cylinder and brought to a final volume of 100 mls with water as before.
The third buffer solution was prepared by weighing 2.68 g of Na2HPO4· 7H2O and placing that in a 125 ml Erlenmeyer flask. Approximately 75 mls of water was added, the solution was swirled until all solids had dissolved and then 5 mls of 1N HCl (provided) was added and mixed. The solution was then transferred to a graduated cylinder and brought to 100 mls as above.
The fourth buffer solution was prepared by pipetting 10 mls of buffer solution 2 into a 100 ml graduated cylinder with a 10 ml plastic pipette. This solution was then brought to a final volume of 100 mls by addition of water.
The fifth buffer solution was prepared by pipetting 10 mls of buffer solution 2 into a 100 mls graduated cylinder as above. This solution was brought to a final volume of 100 mls by addition of 1M NaCl (provided).
Each of the solutions was transferred to a 125 ml Erlenmeyer flask. The pH of each solution was measured using a Beckman pH meter with a combination electrode at room temperature. Just prior to the series of measurements, the pH meter was standardized at pH 7.0 and pH 4.0 using standard buffer solutions (provided). Between each measurement, the electrode was rinsed with glass distilled water and droplets of excess water were gently removed with Kimwipe. At the end of the series of measurements, the pH 7.0 standard buffer was rechecked and was shown to be within 0.04 pH units of pH 7.00. The values of the pH's measured for each of the buffer solutions is given in Table I.
|
Sample |
pH |
|
Buffer Solution 1 |
6.86 |
|
Buffer Solution 2 |
6.87 |
|
Buffer Solution 3 |
6.85 |
|
Buffer Solution 4 |
7.01 |
|
Buffer Solution 5 |
6.38 |
Interpretations
In the preparation of buffer 1, 0.01 moles of NaH2PO4 was added to water and dissolved to form Na+ and H2PO4- ions in solution. (There is also a very small amount of proton dissociation. This significantly decreases the pH of the solution at this point, but has little effect on the concentration of H2PO4-.) Next, 0.005 moles of NaOH was added which dissociated to form Na+ and OH- ions. The OH- and H2PO4- ions then reacted:
(0.005 mole)OH- +(0.01 mole)H2PO4- ®
(0.005 mole)H2O + (0.005 mole)HPO42- + (0.005 mole)H2PO4-
One half of the H2PO4- was converted to HPO42- as shown. The final solution also contained 0.015 moles of Na+.
In the preparation of buffer 2, 0.005 moles each of the monobasic and dibasic sodium phosphate salts were added resulting again in a solution that contained the same concentrations of H2PO4- , HPO42- and Na+ as solution 1.
The preparation of buffer 3 involved reacting 0.01 moles of dibasic sodium phosphate with 0.005 moles of HCl. The H+ that resulted from dissociation of the strong acid reacted with H2PO4- forming water and HPO42-. The resulting solution contained 0.02 moles of Na+, 0.005 moles of Cl-, and again 0.005 moles each of H2PO4- and HPO42-. Note that this solution differs from solutions 1 and 2 in that it contains an extra 0.005 moles of NaCl.
Buffer solution 4 involved a simple dilution. No chemical reaction was involved. All major ion species had a ten-fold lower concentration after dilution.
Buffer solution 5 also involved a ten-fold dilution of the buffer 2 constituents, and the addition of NaCl to a final concentration of 0.90 M.
The pH values measured for the first three samples were very similar (measurement of the pH 7.0 standard buffer before and after the experiment indicated that measurement variations of a few thousands of a pH unit were within the instrument's intrinsic error) and all were significantly lower than the pH predicted from the equation:
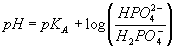
where the acid and base form concentrations are used (not activities). (Since the concentrations of the two forms were the same, one would expect that pH=pKA=7.21.) As explained in the question section, it is possible to correct (at least in an approximate sense) for ion-screening effects in ion solutions using the Debye-Huckle theory. As shown in the questions, an increased ionic strength results in a decrease in the pH of a phosphate buffer solution since the activity coefficient of a doubly charged ion (base form in this case) is always smaller than that of a singly charged ion (acid form in this case) making the last term in the above equation negative. This effect increases with the square root of the ionic strength (see answers to questions). Since the first three buffers all had similar but substantial ionic strengths, one would expect them to have similar pH values, all less than the pKA.
The fourth buffer solution had a much lower ionic strength and thus had a pH closer to the pKA. The fifth buffer had a much larger ionic strength than any of the others and thus had a pH much lower than any of the others.
Answers to the Questions
1)If you compared buffers 1 and 3 you would see that chemically they differ as follows:
(1) 2Na+ + 2H2PO4- + NaOH ® 3Na+ + HPO42- + H2PO4- + H2O
In the first buffer, NaOH (which of course is really Na+ + OH- in solution) is being added to convert half of the H2PO4- to HPO42-. As a result, the final solution has final sodium ion concentration which is 1.5 times the total phosphate concentration. Sodium and phosphate are the only ions. However, in buffer 3:
(3) 4Na+ + 2HPO42- + HCl ® 4Na+ + HPO42- + H2PO4- + Cl-
Here we see that in the end we have an extra sodium ion and an extra chloride ion over what was present in buffer (2). In fact, buffer (3) is buffer (2) plus 50 mM NaCl. It makes a difference how you prepare your buffers!
2) It is a simple matter to calculate ionic strength from the formula
![]()
(1) [Na+] = 150 mM (remember the Na in the NaOH).
[HPO42-] = 50 mM
[H2PO4-] = 50 mM
I=1/2{ (0.150)(1)2 + (0.050)(-2)2 + (0.05)(-1)2} = 0.200 M
(2) [Na+] = 150 mM (two sodiums in Na2HPO4 and one in NaH2PO4).
[HPO42-] = 50 mM
[H2PO4-] = 50 mM
I=1/2{ (0.150)(1)2 + (0.050)(-2)2 + (0.05)(-1)2} = 0.200 M
(3) [Na+] = 200 mM (two sodiums in Na2HPO4).
[HPO42-] = 50 mM
[H2PO4-] = 50 mM
[Cl-] = 50 mM
I=1/2{ (0.200)(1)2 + (0.050)(-2)2 + (0.05)(-1)2 + (0.05)(-1)2 } = 0.250 M
(4) This is just (2) diluted by a factor of 10. Thus, I = 20 mM
(5) For this we have essentially buffer (4) with an additional 0.900 M NaCl
(the NaCl was diluted to 0.9 of its original concentration). Of course the
NaCl dissociates to Na+ and Cl-. Therefore
I = 0.020 + 1/2{ (0.900)(1)2 + (0.900)(-1)2} = 0.920 M
3) and 4) We know that:
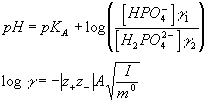
Here, g 1 and g 2 are the activity coefficients for HPO42- and H2PO4-, respectively. m0 is the standard molality which in aqueous solutions at room temperature is essentially 1M. Since in our solutions the concentrations (but not the activities) of the acid and the base are equal
([HPO42- ] = [H2PO4-]), we have:
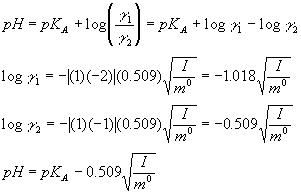
Thus, we can easily predict how pH will depend on ionic strength.
You were only asked to consider buffers (4) and (5) since these should have had the most dramatic effects. However, let's go ahead and make some predictions for each of the buffers. Note that the above equations should be considered as only very rough estimates for buffers with ionic strengths more than 10 or 20 mM. Thus, we will use them in a qualitative, rather than quantitative, way. For all of the buffers, the term containing the ionic strength above is negative and therefore we should see that the pH is lower than the pKA in each case. The first two buffers are the same and should both have pH's that are two or three tenths of a pH unit lower than the pKA (as observed). Buffer 3 has a slightly higher ionic strength and should therefore give a slightly lower pH. This effect would be small (according to the above equation only a few thousands of a pH unit) and thus it is not surprising that we did not see a significant difference in the pH of buffer 3 compared to 1 and 2. Buffer 4 has a much lower ionic strength and should therefore come much closer to the pKA. Actually, at 20 mM, the Debye-Huckle equation is not usually too far off. It results in a pH of about 7.14. The reason why our measured pH was lower may be that at this low concentration of buffer, the buffer capacity is low. This means you are much more sensitive to endogenous acids and bases in the water or on the glassware. One of these is dissolved CO2 which can give water a slightly lower pH than the expected 7.0. The other possible problem may be with the theory itself. A 20 mM ionic strength is still a bit on the high side for Debye Huckle theory. In any case, the theory allows us to rationalize why a higher pH was obtained for (4) than for any of the first three buffers. (5) has the highest ionic strength of all and therefore has the lowest pH. The magnitude of the effect is hard to predict since the theories are extremely inaccurate at high ionic strengths, but it should have been on the order of a half a pH unit lower than number (4).