Science, 28 April 1995, Volume 268, pp. 569-573

How Baseball Outfielders Determine Where to Run to Catch Fly Balls

Michael K. McBeath, Dennis M. Shaffer, Mary K. Kaiser

Current theory proposes that baseball outfielders catch fly balls by selecting a running path to achieve optical acceleration cancellation of the ball.  Yet people appear to lack the ability to discriminate accelerations accurately.  This study supports the idea that outfielders convert the temporal problem to a spatial one by selecting a running path that maintains a linear optical trajectory (LOT) for the ball.  The LOT model is a strategy of maintaining "control" over the relative direction of optical ball movement in a manner that is similar to simple predator tracking behavior.

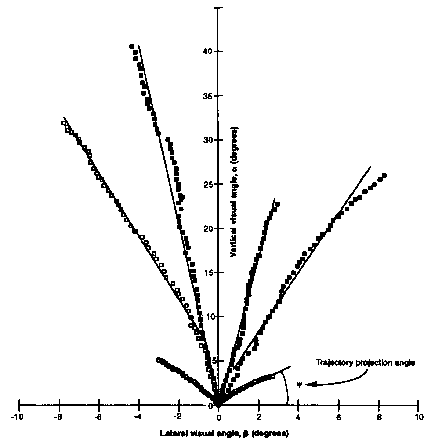
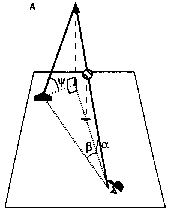
Figure 2.  The LOT model.  This model specifies that fielders "control" the optical direction of ascent of the ball by adjusting their running path to null optical trajectory corvature.  This keeps the image of the ball continuously ascending in a straight line throughout the trajectory.  (A) Fielder optical angle geometry of a ball at an instant in midflight: a = vertical optical angle, b = horizontal optical angle, and Y = optical trajectory projection angle (angle from the perspective of the fielder that is formed by the ball, home plate, and a horizontal line emanating from home plate).  The configuration of Y, a, and bforms a right pyramid such that tan Y = (tan a)/(tan b).  a and b are both controlled to increase continuously throughout the trajectory and are also labeled at time t1 in (B).

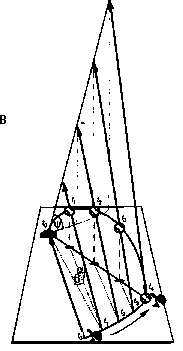(B) Bird's-eye view of a fly ball with a running path that maintains a linear optical ball trajectory (positions shown at times t0 through t4).  If the fielder maintains a constant increase in the lateral optical tangent, tan b, he achieves approximate horizontal alignment with balls that are catchable.  When he runs along a path so that both lateral and vertical tangents increase at a constant rate then the trajectory projection angle Y remains consttant.  Mathematically, the relation is expressed as tan Y = tan a = Caf(t) = CY    tan b     Cbf(t) where Ca, Cb, and CY are constants and f(t) = t = time since trajectory initiation.  In theory, f(t) could be any monotonically increasing function, but for approximately parabolic trajectories, f(t) = t leads to a relatively constant bearing and a near least energy running path.  The fielder scales lateral running speed relative to his distance to home plate, which generally results in a running path that curves slightly.  The resultant optical trajectory is represented behind the ball by the tilted line rising from home plate.

Figure 4.  Results of optical trajectory experiment.  Fielder's view relative to home plate (origin) for typical examples of optical ball position at 1/30-s intervals up to the last half second.  In general, the fielder maintained both vertical and horizontal OAC to achieve a LOT.  The two trials that terminate at a =  (approximately) 5 degree visual angle are line drives, and the other four trials are high fly balls.  The few deviations from continuously rising, straight-line trajectories are cases in which the fielder appeared to adjust and initiate a new linear optical direction partway through the trial (as occurred with the leftmost high fly ball shown).