c) The xz-plane d) The x-axis e) The y-axis f) The z-axis
Intersection with the ![]() plane is the circle
plane is the circle
![]()
It has no intersection with the ![]() plane
plane
Intersection with the ![]() plane is the circle
plane is the circle
![]()
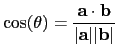
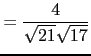
So
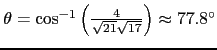 .
.
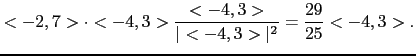
Then point of the turn is
so
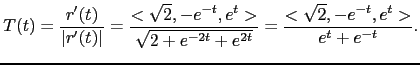
The tangent vector at
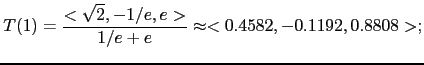
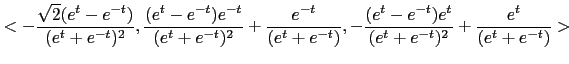 |
|||
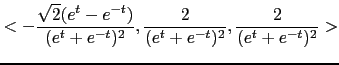 |
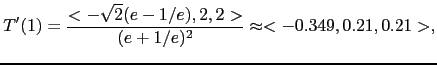
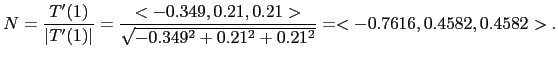
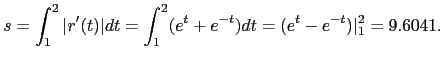
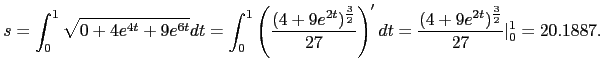
This is a reparameterization of t in 10.8.3 by