Copyright (c) 1989, 1996 Craig W. Kirkwood
All rights reserved.
Aba Manufacturing has contracted to provide Zyz Electronics with printed circuit ("PC") boards under the following terms: (1) 100,000 PC boards will be delivered to Zyz in one month, and (2) Zyz has an option to take delivery of an additional 100,000 boards in three months by giving Aba thirty days notice. Zyz will pay $5.00 for each board which it takes.
Aba manufactures the PC boards using a batch process, and manufacturing costs are as follows: (1) there is a fixed setup cost of $250,000 for any manufacturing batch run, regardless of the size of the run, and (2) there is a marginal manufacturing cost of $2.00 per board regardless of the size of the batch run. Aba must decide whether to manufacture all 200,000 PC boards now or whether to only manufacture 100,000 now and manufacture the other 100,000 boards only if Zyz exercises its option to buy these. If Aba manufactures 200,000 now and Zyz does not exercise its option, then the manufacturing cost of the extra 100,000 boards will be totally lost. Aba believes there is a 50 percent chance Zyz will exercise its option to buy the additional 100,000 PC boards.
For the problem in the preceding question, Aba Manufacturing has created a new option: It can conduct some research and development to attempt to lower the fixed setup cost associated with manufacturing a batch of the PC boards. This research and development would not be completed in time to influence the setup cost for the initial batch that Zyz has ordered, but would be completed before the second batch would have to be manufactured.
The research and development will cost $25,000, and there is a 0.4 probability that it will be successful. If it is successful, then the fixed setup cost per batch will be reduced by $200,000 to $50,000. If the research and development is not successful, then there will be no reduction in the setup cost. There will be no other benefits from the research and development besides the potential reduction in setup cost for the Zyz reorder.
Kezo Systems has agreed to supply 500,000 PC FAX systems to Tarja Stores in ninety days at a fixed price. A key component in the FAX systems is a programmable array logic integrated circuit chip ("PAL chip") which Kezo has bought in the past from an American chip manufacturer AM Chips. However, Kezo has been approached by a Korean manufacturer, KEC Electronics, which is offering a lower price on the chips. This offer is open for only ten days, and Kezo must decide whether to buy some or all of the PAL chips from KEC. Any chips that Kezo does not buy from KEC will be bought from AM.
AM Chips will sell PAL chips to Kezo for $3.00 per chip in any quantity. KEC will accept orders only in multiples of 50,000 PAL chips, and is offering to sell the chips for $2.00 per chip in quantities up to and including 250,000 chips, and for $1.50 per chip in quantities of 300,000 or more chips. However, the situation is complicated by a dumping charge that has been filed by AM Chips against KEC. If this charge is upheld by the U.~S. government, then the KEC chips will be subject to an antidumping tax. This case will not be resolved until after Kezo must make the purchase decision. If Kezo buys the KEC chips, these will not be shipped until after the antidumping tax would go into effect and the chips would be subject to the tax. Under the terms offered by KEC, Kezo would have to pay any antidumping tax that is imposed.
Kezo believes there is a 60 percent chance the antidumping tax will be imposed. If it is imposed, then it is equally likely that the tax will be 50 percent, 100 percent, or 200 percent of the sale price for each PAL chip. Kezo is constantly risk averse with respect to costs with a risk tolerance of $750,000.
In an effort to attract more of Kezo's order, KEC Electronics has revised its offer as follows: At no increase in price, KEC will now provide Kezo with the right to cancel its entire order for a 10 percent penalty after the outcome of the antidumping suit is known. However, KEC will not be able to accept any additional orders from Kezo once the outcome of the suit is known. Thus, for example, if Kezo has agreed to purchase $100,000 worth of PAL chips from KEC, Kezo can cancel the order by paying $10,000.
This ability to cancel the order is potentially of interest to Kezo because it knows that AM Chips would be able to supply PAL chips after the outcome of the antidumping suit is known in time for Kezo to fill the Tarja order. However, Kezo anticipates that AM will increase the price of its chips if an antidumping tax is imposed. In particular, if a 50 percent tax is imposed, then it is equally likely that AM will increase its chip prices by either 10 or 20 percent. If a 100 percent tax is imposed, then it is equally likely that AM will increase its chip prices by 10, 20, or 30 percent. Finally, if a 200 percent tax is imposed, it is equally likely that AM will increase its chip prices by 10, 20, 30, or 40 percent.
Assume that all other information given in the preceding question is still valid while answering the questions below.
arthill Industries, a food grower with diversified worldwide operations, faces a possible drought at its U. S. Midwest soybean operation. If rain falls immediately, then Carthill knows that it will be able to sell its soybean crop for $10 million next autumn. However, if the drought continues, some of its soybeans will be lost. In particular, the fraction of the soybeans lost will increase as the square of the time that the drought lasts up to three months. If the drought lasts for three months or longer, then Carthill's entire soybean crop will be lost. But, if the drought continues, then the price of soybeans will increase. In particular, the price will increase linearly with the length of time until rain comes. If rain is delayed for three months, then the price of soybeans will triple. Regardless of how long the drought continues, Carthill's costs associated with the soybean crop will be the same because of its "no layoff" policy.
Given these facts, it is possible that Carthill's revenue will actually increase because of the drought. For example, if the drought continues for exactly two more months, Carthill's production will be reduced by 2 * 2/9 = 4/9, but the price will increase by a factor of 1 + (2/3) * 2 = 7/3. Therefore, Carthill's revenue from the soybean crop in this case will be
$10 million * [1-(4/9)] * (7/3) = $10.37 million.
Agricultural Distributors, Ltd. has offered to contract with Carthill to buy Carthill's entire soybean crop (whatever the amount turns out to be) for a fixed price of $10 million payable upon delivery of the soybeans. This offer is only open for three more days, and Carthill must decide whether to accept the offer.
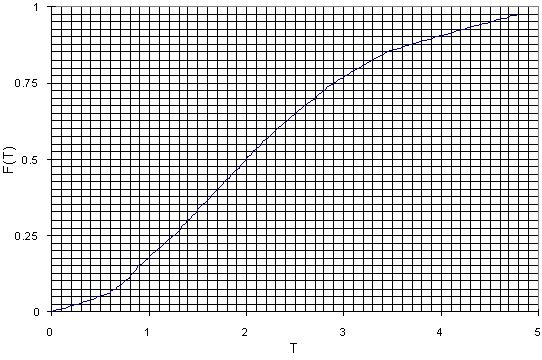
After conducting the analysis in part a, Carthill assesses the cumulative probability distribution shown below for the time T until the drought ends.

Download Excel spreadsheet for this graph.
To analyze whether Carthill should accept Agricultural Distributors' offer, you will approximate the continuous distribution for T by discrete probability distributions. Three methods that are often used to do this are (1) the "5/50/95" method where the distribution is approximated by the 0.05, 0.50, and 0.95 fractiles of the continuous distribution with probabilities of 0.185 assigned to the 0.05 and 0.95 fractiles; (2) the "10/50/90" method where the distribution is approximated by the 0.10, 0.50, and 0.90 fractiles with probabilities of 0.25 assigned to the 0.10 and 0.90 fractiles; and (3) the "equally probable interval" method where the range of the distribution is split into a number of intervals, each with the same probability, and each interval is approximated by the median of the interval.
J. R. Rich is a constantly risk averse private investor with a discount rate of 15 per cent per year and a risk tolerance of $200 thousand. He has $2 million in spare cash which he wishes to invest for two years. (At the end of two years, he will need the money for a project that is now in the early planning stages.) He had been planning to invest the money in a two year certificate of deposit (CD) at 14 percent per year compounded annually. However, just before buying the CD, he was approached by a real estate developer who wishes to obtain a one year loan of the $2 million. J. R. has thoroughly investigated the real estate developer, and has determined that there is no chance of losing his money if he loans it to the developer. However, while he is sure the developer is willing to offer a higher interest rate than the CD interest rate, the problem is that J. R. will have to find a place to invest the $2 million during the second year. He believes that interest rates are going to drop, and that he will only be able to obtain a rate of between approximately 10 and 15 percent per year on a one year investment for the second year. Whatever he puts his money into during the second year, he will invest both the principal and the interest earned during the first year.
 Return to ASU decision analysis and system dynamics resources page. [2020-10-02]
Return to ASU decision analysis and system dynamics resources page. [2020-10-02]