Hemoglobin
Cooperativity
and Binding
It is often the
case that biochemical systems require tighter control than can be achieved with
the sort of simple affector system that is based on just a single linear
binding event. Often one needs a response more like a switch -- little effect
at low concentration then a rapid rise to maximal activity. A classic example
has to do with the protein hemoglobin which binds oxygen in your lungs and
carries it to other tissues of your body. The problem is simply this, in the
lungs you want hemoglobin to bind oxygen tightly so that a large fraction of
the hemoglobin will pick up an oxygen before cycling back through the other
tissues. However, in the other tissues, one wants hemoglobin to bind oxygen
loosely so that it can be easily relinquished for use in respiration. How do we
control the binding? Obviously the oxygen concentration in the blood near the
lungs is going to be higher than it is in tissues were oxygen is rapidly being
used up. But the difference is not large enough to cause nearly complete
binding in the lungs and nearly complete oxygen release in the other tissues. A
curve describing the fraction of hemoglobin molecules bound to oxygen as a
function of the oxygen concentration is calculated assuming the sort of simple
equilibrium binding model we discussed before is as follows: 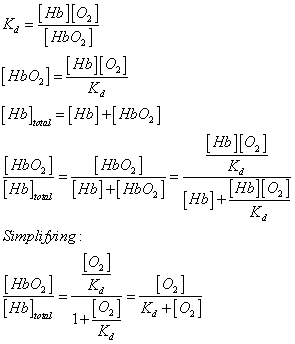
where Kd is the dissociation
constant, [Hb] is the free hemoglobin concentration, and [Hb]t is the total hemoglobin
concentration. The final equation should look very familiar to you. The
dissociation constant, Kd, is
just a backwards equilibrium constant.
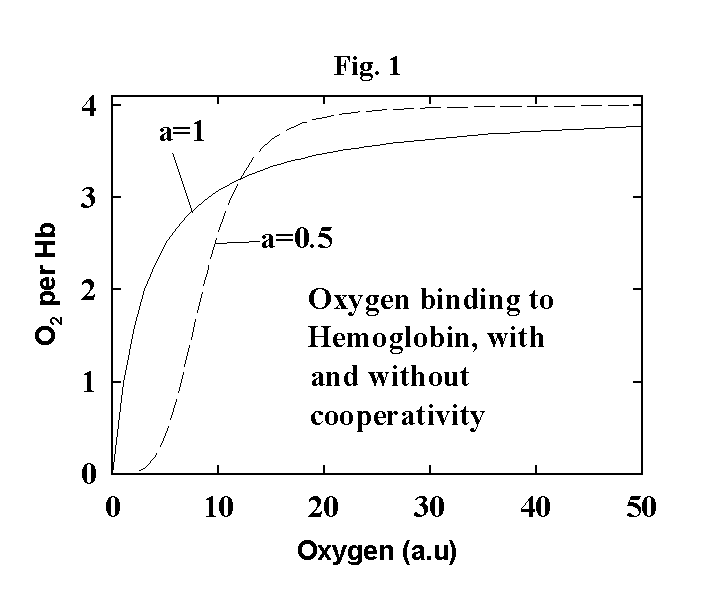
Now if this was the
whole picture, a plot of the fraction of Hb with oxygen bound to it would look
like the solid line in Fig. 1 (see below -- this is just a plot of the equation
above after dividing both sides by the total amount of Hb). What we can see is
that the curve is not very sharp. That is, it takes a relatively large change
in the oxygen concentration in the blood to cause a significant uptake or
release of oxygen from Hb. We would like a finer switch, where a small change
in oxygen concentration resulted in going from almost all Hb in the unbound
state to almost all Hb in the bound state.
Nature has come up with an interesting solution to this problem which is called
cooperativity. Hb is actually a tetramer of four subunits each of which can
bind an oxygen. This binding is cooperative, that is, the binding of the first
oxygen makes binding of the second more favorable which makes binding of the
third even more favorable which makes binding of the fourth even more
favorable. Lets draw a picture of this:
Four successive oxygen molecules are bound to hemoglobin and each time one
binds the dissociation constant for the next one decreases by a factor a.
Remember that a lower dissociation constant means tighter binding. What does
this do to the fraction bound vs. oxygen concentration curve? Let's work
through it first with a simpler case. Consider:
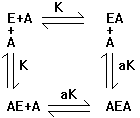
We want to know how
many A's are bound per E (the occupancy of A on E).
![]()
Here N is the
number of A's bound per enzyme. This is equal to all bound forms of A (remember
there are two possible sites for A on E that are distinguishable resulting in
AE and EA). The AEA term is multiplied by 2 because it contains two bound A
molecules. Et is the total enzyme concentration. It equals all forms of both
the free enzyme and enzyme bound to A. In this case AEA term is not multiplied
by two since we are interested in the number of enzyme molecules represented in
the AEA complex.
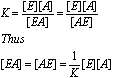
Remember that K
defined in this way is a dissociation constant, the inverse of a normal
equilibrium constant. It is often written as Ks or Kd to avoid confusion, but I
will just refer to it as K here. Cooperativity is represented by multiplying
the dissociation constant by the factor a when considering binding of the
second A to E. If a=1 there is no cooperativity. If a<1 then binding of the
second A is stronger than the first. If a>1 then binding of the second A is
weaker than the first. We can see that
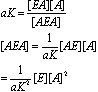
Solving for the
occupancy of A on E: 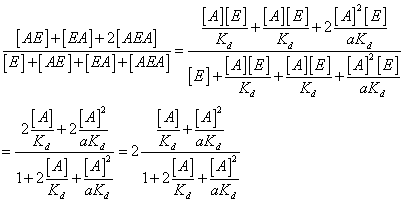
Now if a=1 (no
cooperativity) this reduces to
![]()
which is essentially the same as the simple equation for Hb binding to one O2 except that it is
multiplied by two because two A's can bind per E.
What the
cooperativity does, however, is it makes the terms with [A]2 much
more important. For positive cooperativity,
a<1 and therefore the terms with a in the denominator become larger. This makes the curve in Fig. 1 look more like
a parabola at low [A] instead of a straight line. The result is a sigmoidal curve with a
sharper dependence on the concentration of A.
If we now consider a more realistic situation with hemoglobin which has four
total binding sites, the situation becomes a bit more complex. We must again
remember that the four binding sites are distinguishable, and therefore we must
consider all forms of singly, doubly, triply and quadruplely bound hemoglobin:
Note that there are
four possible ways for one O2 to be bound, six ways for two, four ways for three
and only one way for four O2's to be bound. As before, we can write the
concentration of one bound, two bound, three bound or four bound species in
terms of the concentration of Hb and O2 by using the dissociation constant, K, and the
cooperativity factor, a:
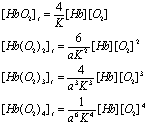
This is more
complicated than the case for two ligands binding, but you can see the pattern
is the same. The expression for N, the
number of O2's bound per hemoglobin (the
occupancy) is:
![]()
substituting the
expressions for the different bound forms of hemoglobin into the above equation
yields (after some simplification):
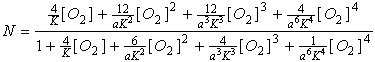
For a = 1 (no
cooperativity) this factors into:
![]()
as one might expect
for a four binding site molecule with no cooperativity. We can also consider
what happens if a is significantly less than 1. In this case, only the higher
order terms become significant and we have:
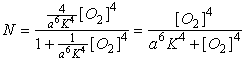
The resulting plot is shown as the dashed line in Fig. 1. As you can see, there
is now a much smaller change in oxygen concentration required to go from mostly
bound to mostly unbound. Positive cooperativity of substrate binding is a very
common method for causing the control of a reaction or process to be much more
sensitive to the substrate concentration.
As practice please
do the following problem:
1) The repressor of
lambda phage is a dimer in its active form (if you want to read about lambda
repressor you can look it up in any biochem text book). This is true of a
number of regulatory proteins. Consider the chemical interactions between a
regulator and an operator diagrammed below (if you don't know what an operator
is, it doesn't really matter, just consider it as something that R binds to):
Case 1:
![]()
Case 2:
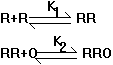
where K, K1 and
![]()
The definition of
the fraction of the operator with dimer regulator bound in case 2 is:
![]()
Make a sketch of
these two functions showing how the binding curve differs in the case of a
dimer regulator from that of a monomer. Why is this difference important to the
gene regulation of bacteriophage lambda?