Tensor Completion for Weakly-Dependent Data on Graph for Metro Passenger Flow Prediction
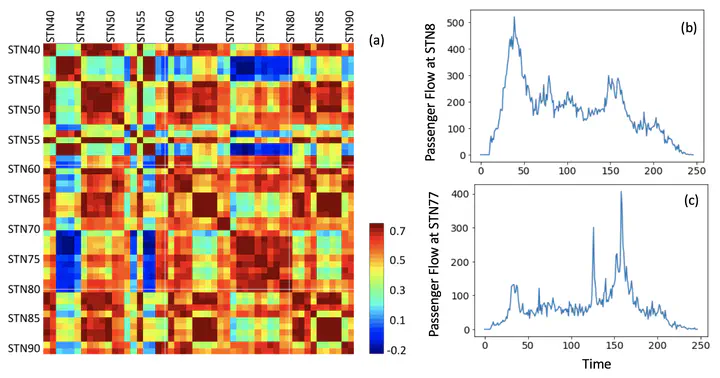 Different Spatial and Temporal Structures
Different Spatial and Temporal Structures
Abstract
Low-rank tensor decomposition and completion have attracted significant interest from academia given the ubiquity of tensor data. However, the low-rank structure is a global property, which will not be fulfilled when the data presents complex and weak dependencies given specific graph structures. One particular application that motivates this study is the spatiotemporal data analysis. As shown in the preliminary study, weakly dependencies can worsen the low-rank tensor completion performance. In this paper, we propose a novel low-rank CANDECOMP / PARAFAC (CP) tensor decomposition and completion framework by introducing the $L_1$-norm penalty and Graph Laplacian penalty to model the weakly dependency on graph. We further propose an efficient optimization algorithm based on the Block Coordinate Descent for efficient estimation. A case study based on the metro passenger flow data in Hong Kong is conducted to demonstrate improved performance over the regular tensor completion methods.